Математическая модель дробления и взрыва метеорных тел в атмосфере
Г.А. Тирский, Д.Ю. Ханукаева
Институт механики МГУ им. М.В.Ломоносова, Москва Несмотря на то, что в настоящий момент факт механического дробления Тунгусского космического тела (ТКТ) и других крупных метеороидов во время полета в атмосфере не подвергается сомнению, единой модели этого явления до сих пор нет. Существующие модели фрагментации метеороидов можно условно разбить на следующие идеологические группы: квазинепрерывное дробление, катастрофическое разрушение тела (гидродинамические модели), прогрессивное дробление. Подробный обзор указанных моделей имеется в работе [1]. Модели первой группы можно отнести к идеологически «ранним». Модели гидродинамической группы, по-видимому, хорошо описывают поведение только особо крупных однородных тел, к которым можно отнести и ТКТ, и иногда мелких, но чрезвычайно малопрочных. Модель прогрессивной фрагментации, развиваемая в данной работе, описывает схему последовательного дробления космических тел на несколько фрагментов, в соответствии с которой распадается большинство наблюдаемых метеороидов. Механизм катастрофического разрушения содержится в ней как предельный случай.
Однако ни одна из упомянутых моделей не дает удовлетворительного объяснения неоднократно наблюдавшихся концевых вспышек мелких и теплового взрыва крупных метеороидов и, в частности, взрыва ТКТ. Под взрывом будем понимать быструю (за доли секунды), происходящую в узком интервале высот (менее 1 км) передачу энергии раздробленного метеороида атмосфере и превращение всей его массы в пар. Это условие равносильно тому, что кривая погонной потери кинетической энергии тела с высотой имеет резкий максимум, сосредоточенный в узком интервале высот, до сих пор не полученный ни в одной из работ, посвященных взрыву метеороидов. В данной работе на заключительной стадии движения раздробленного метеороида учитываются термонапряжения, что позволяет получить узкий максимум энерговыделения, означающий наличие взрыва.
В работе [2] было получено аналитическое решение системы основных уравнений физической теории метеоров [3] в рамках модели прогрессивного равновесного дробления тела переменной массы под действием аэродинамической нагрузки rV2 (r - плотность воздуха, V - скорость тела). Показано, что начавшееся лавинное разрушение метеороида будет продолжаться вплоть до достижения скоростным напором своего максимума, положение и величина которого находятся с помощью полученного решения, а также определяются число, масса и размер осколков в этот момент [2]. Дальнейшее дробление возможно, но уже под действием термонапряжений, которые возникают из-за больших перепадов температуры во всем объеме мелких осколков и пропорциональны квадрату их размеров. Указанные напряжения могут превысить предел прочности образовавшихся осколков и повлечь их разрушение до размеров крупной пыли, которая быстро испаряется в раскаленном газовом облаке, то есть «взрывается». Если же размеры образовавшихся фрагментов недостаточно малы для начала термического разрушения, на поверхность планеты выпадает метеоритный дождь.
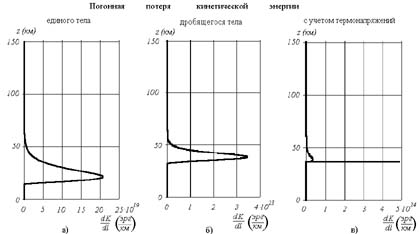
На рисунке приведен пример расчета погонной потери кинетической энергии тела с высотой в рамках модели единого тела (а), дробящегося тела без учета (б) и с учетом термонапряжений (в). Все они построены по входным параметрам ТКТ: скорость Ve=35 км/с, масса Мe=109 кг, плотность d=103 кг/м3, угол наклона траектории к горизонту q=30°, прочностные характеристики были подобраны в соответствии с данными наблюдений по высотам начала и окончания дробления [4].
Таким образом, предложена математическая модель дробления и концевого теплового взрыва болидов, более адекватно объясняющая наблюдательные данные, связанные не только с ТКТ, но и с разрушением других метеороидов. Работа поддержана грантами РФФИ №03-01-00-542, №03-01-06-179. Литература
dukh@imec.msu.ru