Определение массы входа крупных болидов
В.П.Стулов
Институт механики МГУ им. М.В.Ломоносова
stulov@imec.msu.ru
Одной из фундаментальных проблем метеорной физики является определение доатмосферной массы болидообразующих тел. Интенсивность метеорного явления определяется кинетической энергией тела при подходе к внешней атмосфере планеты. Как известно, скорость тел при входе в атмосферу Земли лежит в относительно узком диапазоне 11 < Ve < 72 км/с, так что разброс значений скоростного вклада в кинетическую энергию не превышает 50 раз. Вместе с тем значение массы метеорного тела может изменяться в существенно более широком диапазоне, от долей грамма (микрометеоры) до сотен тысяч тонн (Тунгусское космическое тело), т. е. на 12-14 порядков. Кроме того, скорость входа сравнительно просто определяется в наблюдениях начального участка атмосферной траектории. Напротив, надежные способы определения массы входа, содержащие оценку точности результата, в настоящее время отсутствуют.
Обзор существующих методов
Известные из литературы подходы к оценке массы входа можно условно разделить на две группы. В первую входят так называемые фотометрические методы, использующие светимость болида. Чаще всего встречается метод определения фотометрической массы Mph по формуле
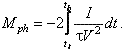
Здесь I — интенсивность свечения вдоль наблюдаемого участка траектории, tb, tt — начальное и конечное время для этого участка, — коэффициент пропорциональности. Формула (1) основана на предположении, что определяющий вклад в светимость дают пары материала тела. Детальные расчеты показывают, что это нельзя считать обоснованным, особенно для крупных тел.
Другой подход, основанный на величине светимости, разработан И.В.Немчиновым с сотрудниками и назван методом радиационного радиуса (ссылки на оригинальные работы имеются в [1]). С использованием метода нестационарной аналогии авторы рассчитали таблицу светимости в зависимости от радиуса тела, скорости и высоты полета. Радиус наблюдаемого тела определяется затем по этой таблице по величине наблюдаемой светимости при тех же значениях скорости и высоты полета.
Другую группу методов можно считать динамическими, поскольку в них масса тела определяется по эффекту торможения в атмосфере. Решение уравнений метеорной физики [2] содержит два безразмерных параметра: a (баллистический коэффициент) и b (параметр уноса массы)
(2)
Параметр определяет область максимального торможения в атмосфере. Поскольку он дважды содержит размер тела (Se и Me), его удобно переписать так
(3)
где Ae — коэффициент формы тела.
В динамических методах параметр a определяется (3) путем сравнения расчетной траектории с наблюдаемой. После этого при заданных Ae и плотности тела rm по формуле (3) определяется Me. Недостатком такого подхода является именно необходимость априорного задания величин Ae и m, которые в наблюдениях не определяются.
Динамический подход, основанный на решении для траектории в переменных v, y (безразмерные скорость и высота) и методе наименьших квадратов, использовался нами ранее [2]. Другой подход, учитывающий дробление, предложен авторами [3] и назван ими методом гросс-фрагментации.
Ниже приводятся фактические данные по определению массы входа болида Бенешов (EN070591) динамическими и фотометрическими методами.
Сведения о болиде Бенешов
Наблюдение и регистрация болида Бенешов были проведены станциями Чешской части Европейской болидной сети 7 мая 1991 года. По мнению одного из наблюдателей [4], это был один из наиболее ярких и детально документированных болидов. Начиная с высоты 42 км, наблюдалось отделение фрагментов от основного тела. Всего до достижения высоты 24 км отделилось 4 фрагмента, первый из которых в процессе движения, в свою очередь, разделился надвое. На высоте 24 км произошло окончательное дробление основного тела на три крупных и множество мелких осколков. Полное погасание болида произошло на высоте 19 км при скорости все еще компактного роя V = 5.2 км/с [5]. Краткая характеристика болида приведена в таблице 1.
Таблица 1
|
Параметры светящегося участка траектории, начало/конец |
Средний угол с горизонтом, |
Фотомет-рич. масса, |
Длина траект., |
Продол-житель., |
Источник | |
|
Скорость, км/c |
Высота, км |
град. |
кг |
км |
сек |
|
|
21.09/2.0 |
97.72/16.05 |
- |
15000 |
82.8 |
5.2 |
[4] |
|
21.18/4.9 |
90.71/16.72 |
80.6 |
13000 |
75.0 |
4.5 |
[5] |
Определение массы входа болида Бенешов
Решение задачи о траектории болида Бенешов методом наименьших квадратов показало, что наилучший результат дает модель единого тела с учетом абляции, при этом = 7.8,
= 1.5. Оценка взаимной роли дробления и абляции обнаружила, что при Me = 28 кг унос массы абляцией составил 15.8 кг, а суммарный унос массы в наблюдавшихся фрагментах составил 7.2 кг.
Результаты оценки массы входа болида Бенешов фотометрическими и динамическими методами сведены в таблицу 2.
Таблица 2
|
Метод |
наблюдения, Mph |
наблюдения, Mph |
метод радиационного рад. |
метод гросс-фрагментации |
метод наименьших квадратов |
|
Источник |
[4] |
[5] |
[1] |
[3] |
данная работа |
|
Me, кг |
15000 |
13000 |
3000-4000 |
82 |
сфера: 28; плита 1х1х0.5: 523 |
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проект 02-01-00204.
Литература
- Borovicka J., Popova O.P et al. Astron. Astroph. 1998, v. 334, p. 713-728
- Стулов В.П., Мирский В.Н., Вислый А.И. Аэродинамика болидов. М.: Наука, 1995
- Ceplecha Z., Spurny P., et al. Astron. Astroph. 1993, v. 279, p. 615-626
- Spurny P. Planet Space Sci. 1994, v. 42, № 2, p. 157-162
- Borovicka J., Spurny P. Icarus 1996, v. 121, p. 484-510
