Тунгусский феномен / Исследования / Конференции / 100 ЛЕТ ТУНГУССКОМУ КОМЕТНОМУ ТЕЛУ, Санкт-Петербург, 25 марта 2008 г. / Материалы Конференции / I. ОРБИТА И ТРАЕКТОРИЯ

А.С. Заботин, Ю.Д. Медведев
Институт прикладной астрономии РАН, 191187,СПб, наб. Кутузова 10,
E-mail: medvedev@ipa.nw.ru

О ВОЗМОЖНОЙ ГЕЛИОЦЕНТРИЧЕСКОЙ ОРБИТЕ ТУНГУССКОГО МЕТЕОРИТА
ДО ЕГО ВХОЖДЕНИЯ В АТМОСФЕРУ ЗЕМЛИ

Аннотация. Численно исследована ретроспективная эволюция орбиты тунгусского метеорита от момента его взрыва до входа в атмосферу Земли. В модель движения метеорита включены гравитационные ускорения от Земли, Луны и Солнца, а также ускорения, возникающие из-за торможения тела в атмосфере Земли. Учитывалась возможность дробления и горения тела в атмосфере. В качестве начальных условий были взяты место и время взрыва тунгусского метеорита. Варьировались значения величины модуля, азимута и наклона вектора скорости к поверхности Земли, а также высота взрыва метеорита. Кроме того, исследовалось влияние размеров, механических и теплофизических характеристик тела на его движение. Численные эксперименты показали, что лучше всего наблюдательным данным метеорита удовлетворяют небольшие значения величины модуля и наклона вектора скорости к поверхности Земли при его движении в атмосфере. При таких начальных данных метеорит может совершить один или даже несколько оборотов вокруг Земли до своего падения. Гелиоцентрические орбиты, получающиеся при моделировании с такими начальными данными, до входа метеорита в атмосферу Земли во многом близки к орбите астероида Apophis.

Это позволяет говорить о достаточно частых сближениях астероидов типа Apophis с Землей и их падениях на Землю.

Введение

Исследованию динамики тунгусского тела и обстоятельств его взрыва посвящено большое количество публикаций, обзор которых приведен в монографии Н.В. Васильева [Васильев, 2004].

Наиболее вероятным сценарием этого явления, объясняющим большинство наблюдений, является проникновение в атмосферу Земли небесного тела достаточно большого размера - до нескольких сотен метров в диаметре. В результате торможения этого тела в атмосфере, оно раздробилось и затем взорвалось, не долетев до поверхности Земли. К настоящему времени собрано большое число фактов, относящихся к этому явлению; наиболее достоверными, на наш взгляд, являются следующие:

1) Взрыв произошел во вторник 30 июня 1908 г. в 00 час.14,5±1,0 мин. по Гринвичу или в 7 час 14,5 минут утра местного времени. Момент был получен из обработки сейсмо- и барограмм [Гольдин, 1986].

2) На месте предполагаемого взрыва имеется вывал леса, обнаруженный Л.А. Куликом [Кулик, 1927]. Географические координаты центра вывала леса, над которым предположительно располагался эпицентр взрыва, следующие: 60°52' 08'' северной широты и 101° 55' 03'' восточной долготы. Площадь вывала леса из-за взрыва составляет 2150 км2 [Васильев, 2004].

3) Акустические и световые явления распространились на площади свыше одного миллиона квадратных километров с радиусом около 800 километров. После взрыва практически на всей Земле фиксировались явления, связанные с большим количеством пыли в атмосфере [1].

4) Высота взрыва приблизительно 10 км. [Васильев, 2004]

5) Направление движение болида: величина азимута лежит в диапазоне ( ), величина угла наклона к горизонту колеблется, по разным источникам, от до [Васильев, 2004].

Следует обратить внимание на большой разброс в значениях азимута, который обусловлен противоречивыми на первый взгляд наблюдениями двух групп. Так называемая «южная» группа очевидцев - респонденты Иркутской обсерватории и «восточная» - очевидцы с верховья р. Нижней Тунгуски. Противоречивость заключается в том, что из наблюдений «южной» группы очевидцев следует, что тело двигалось в атмосфере с юга на север. Если учесть наблюдения очевидцев с верховья р. Нижней Тунгуски, в основном охотников и поэтому не имеющих возможности уверенно говорить не только о времени, но даже о дате наблюдений, то получается, тело двигалось с востока на запад. Последнее обстоятельство породило большое количество фантастических гипотез. Однако, на наш взгляд, это противоречие может быть разрешено, если предположить, что тунгусский болид несколько раз входил в земную атмосферу, т.е. тунгусский метеорит был временным спутником Земли. Тогда траектория первого прохождения тела через атмосферу должна проходить из-за вращения Земли восточнее, чем последующие. Вероятней всего тунгусское тело два раза входило в атмосферу Земли. Поэтому световые и звуковые явления первого прохождения, соотнесенные с местом падения, дают движение тела с востока на запад. Возможность нахождения тела на орбите временного спутника Земли была показана нами в работах [Медведев, 1997; Бывшев, Медведев, 1997]. Проведенные в этих работах исследования показали, что лучше всего наблюдательным данным метеорита удовлетворяют небольшие значения величины модуля и наклона вектора скорости к поверхности Земли при его движении в атмосфере. Показано, что при таких начальных данных метеорит может совершить один или даже несколько оборотов вокруг Земли до своего падения. Гелиоцентрические орбиты, получавшиеся при моделировании с такими начальными данными, оказались во многом близки к орбите Земли.

Поэтому, когда был открыт астероид Apophis, орбита которого также близка к орбите Земли, нами было решено продолжить исследования, сделав упор на вычисление возможных орбит тунгусского тела до его вхождения в атмосферу Земли.

Описание модели

Как и в предыдущих исследованиях численно исследовалась ретроспективная эволюция орбиты тунгусского метеорита от момента его взрыва до входа в атмосферу Земли. При моделировании были сделаны следующие предположения:

• Ядро болида имеет сферическую форму, постоянную плотность и однородный химический состав.

• Ядро остается единым, но может претерпевать поверхностное разрушение, сохраняя при этом исходную сферическую форму.

• Не учитываются различия градиентов сил и параметров среды в разных частях ядра и влияние вращения ядра на его поступательное движение.

• Предполагается, что часть энергии, возникающей из-за работы силы сопротивления атмосферы, идет на разогрев и испарения вещества метеорита, что приводит к уменьшению размеров ядра болида, при этом оно сохраняет сферическую форму.

• В движении болида учитываются возмущения от гравитационного поля Земли, сопротивления атмосферы и притяжения Луны и Солнца.

На основании сделанных предположений уравнения движения тела имели вид:

, (1)

Здесь - сила гравитационного притяжения Земли, при расчетах Земля аппроксимировалась сжатым сфероидом, поэтому эта сила бралась в виде:

, (2)

где - гравитационная постоянная, - масса Земли, - масса болида, - геоцентрический вектор положения болида, и - вторая зональная гармоника и радиус Земли, - угол, отсчитываемый от плоскости экватора Земли.

- сила сопротивления атмосферы:

, (3)

где - коэффициент, зависящий от аэродинамических характеристик болида, - радиус болида, - плотность атмосферы, - скорость болида относительно атмосферы.

, - гравитационное притяжение Луны и Солнца, которые брались в виде:

, (4)

где , - массы Луны и Солнца, , - расстояние между болидом и Луной и между болидом и Солнцем, , - геоцентрические вектора положения Луны и Солнца.

При расчете силы сопротивления среды учитывалось, что часть энергии, генерируемой внутри ударного слоя, передается поверхности тела, вызывая ее разогрев и сублимацию вещества. Это, в свою очередь, вызывало изменение массы и миделева сечения небесного тела во время его движения в атмосфере Земли. Для учета изменения радиуса болида из-за испарения в атмосфере Земли использовалось следующее дифференциальное уравнение:

, (5)

где - доля энергии, идущей на испарения вещества поверхностного слоя болида, - плотность болида, - количество энергии, требующееся на испарение единицы веса вещества болида. Последнее дифференциальное уравнение было получено из следующих соотношений. Из ранее принятых предположений следует, что между работой силы сопротивления и энергией, идущей на испарения вещества, имеет место равенство:

, (6)

где - масса поверхностного слоя, которая вычисляется по формуле

. (7)

Подставляя (7) в (6) и переходя к пределу в конечных разностях и , получаем дифференциальное уравнение (5).

Кроме того, учитывалась поверхностная фрагментация ядра болида. Учет происходил путем повышения величины абляции в момент, когда давление на переднюю точку

тела достигало критического значения ( ). Увеличение абляции происходило в раз. Выбор именно такого коэффициента был обусловлен следующими соображениями. В работе [Hills, Goda 1997] построена иерархическая модель фрагментации тела, согласно которой тело может разрушаться в несколько стадий, при этом каждый раз образуются наибольший осколок и множество более мелких. Сценарий разрушения следующий. При превышении критического значения давления на переднюю точку тела, происходит сброс вещества с его поверхности. Наибольший фрагмент и более меньшие осколки составляют единый аэродинамический объект. Когда вследствие разбегания осколков, радиус облака составит около двух начальных радиусов тела, происходит потеря облаком осколков аэродинамической связи с наибольшим по массе осколком. После этого процесс повторяется. Между скоростью разбегания осколков и скоростью тела относительно атмосферы существует следующее линейное соотношение [Hills, Goda 1997]:

. (8)

Коэффициент в выражении (8) принят нами как коэффициент усиления величины абляции для моделирования процесса фрагментации.

Математическая модель, описывающая движение болида и изменение миделева сечения тунгусского метеорита, представляет собой систему дифференциальных уравнений 7-го порядка (3 уравнения движения 2-го порядка и уравнение, описывающее изменение радиуса ядра болида из-за абляции). Эта система интегрировалась методом Рунге-Кутта 7(8) порядка. Положение Луны и Солнца задавалось эфемеридой DE-403. Изменение плотности атмосферы Земли с высотой было представлено в виде трех экспоненциальных слоев с верхними границами на 25, 120 и 500 км от поверхности Земли соответственно. Рассматривалась ретроспективная эволюция, т.е. задались начальные данные в момент взрыва и система интегрировалась назад по времени. Это, в частности, приводило к увеличению размеров ядра болида при интегрировании. Была составлена соответствующая программа, входными параметрами которой были величины, приведенные в Табл.1.

Табл.1 Входные параметры программ

Параметр	Значение
Начальный момент (юлианская дата и дробная часть, соответствующая моменту взрыва).	2418122.51015^*
Интервал интегрирования (в сутках)	30.0
Высота тела в начальный момент (высота взрыва, в км)	10.
Широта (в градусах и долях градуса)	60.9^*
Долгота (в градусах и долях градуса)	101.9^*
Модуль скорости (в км/с)	8.2
Азимут вектора скорости (в градусах и долях градуса)	180.0
Высота вектора скорости (в градусах и долях градуса)	-3.0
Радиус ядра (в км)	0.1
Плотность вещества ядра (в г/см³)	1.0
Теплота сублимации вещества (в кал/г)	1000.0
Критическое давление вещества (в 10⁶ Па)	100.0
Коэффициент лобового сопротивления	2.0
Коэффициент передачи энергии на сублимацию	0.001

Звездочками обозначены величины, которые не варьировались при модельных вычислениях, поскольку они достаточно точно известны из наблюдения.

Численное моделирование

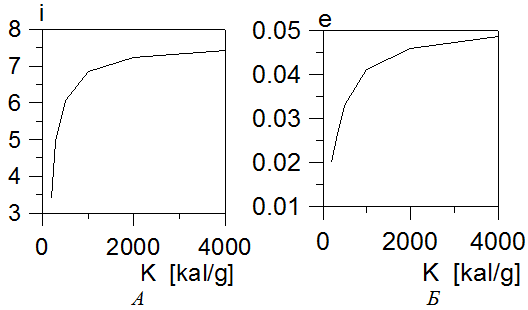
Исследовалось влияние, приведенных в Табл.1 величин на параметры орбиты болида. Мы приводим данные о влиянии величины теплоты, идущей на испарения 1 г вещества ядра болида , на параметры гелиоцентрической орбиты и радиус ядра болида. Результаты приведены в виде рисунков (Рис.1и 2).

Рис.1 (А и Б). Изменение наклона гелиоцентрической орбиты болида i (рис. А) и изменение эксцентриситета гелиоцентрической орбиты болида e (рис. Б) с теплотой сублимации вещества его ядра K.

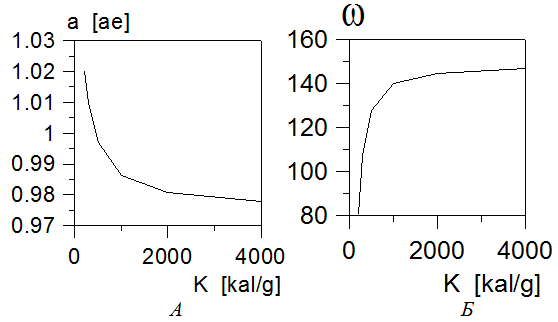
Рис.2 (А и Б). Изменение большой полуоси гелиоцентрической орбиты болида a (рис.А) и изменение угла перигелия ω (рис. Б) с теплотой сублимации вещества его ядра K.

Результаты моделирования показывают, что увеличение величины приводит к росту величин наклона, эксцентриситета и аргумента перигелия гелиоцентрической орбиты до входа метеорита в атмосферу, а значение большой полуоси уменьшается с ростом величины . Здесь следует отметить, что все остальные параметры принимались равными величинам, приведенным в Табл.1. При значении значение элементов орбиты метеорита близки к значению элементов орбиты Apophis, за исключением долготы восходящего узла орбиты, величина которой практически не меняется и остается равной , что соответствует долготе Земли на момент тунгусского явления. Для сравнения в Табл.2 приведены элементы орбиты астероида Apophis.

Таблица2. Элементы орбиты астероида ( 99942) Apophis

ω	Ω	i	e	N	a
126.39517	204.45715	3.33128	0.1910744	1.11277902	0.9222814

На рис. 3 приведена зависимость величины радиуса ядра болида до его вхождения в атмосферу с теплотой, требуемой на сублимацию одного грамма вещества, при предположении, что в момент взрыва ядро было радиусом 0.1 километра.

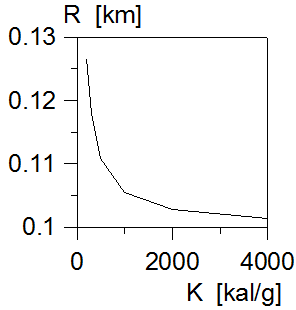
Рис.3. Изменение радиуса ядра тунгусского болида R с теплотой сублимации вещества его ядра K.

Рис. 3 показывает, что при небольших значениях величины тунгусское тело уменьшается приблизительно на 25 % в диаметре из-за испарения и частичного разрушения.

Кроме того, исследовано влияние радиуса болида в момент взрыва на элементы орбиты. Результаты приведены на рисунках 4 и 5.

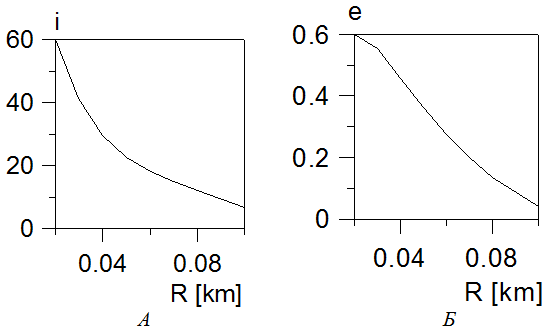
Рис.4 (А и Б). Изменение наклона гелиоцентрической орбиты болида i (рис.А) и изменение эксцентриситета гелиоцентрической орбиты болида e ( рис.Б) с радиусом его ядра R.

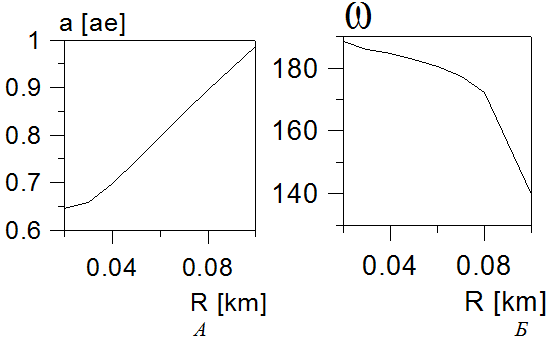
Рис.5 (А и Б). Изменение большой полуоси гелиоцентрической орбиты болида a (рис.А) и изменение угла перигелия ω( рис.Б) с радиусом его ядра R.
Рисунки 5 и 6 показывают, что уменьшение радиуса болида более существенным образом влияет на его гелиоцентрическую орбиту до входа в атмосферу, чем величина K. При небольших размерах тела в момент взрыва гелиоцентрическая орбита становится близкой к кометной, несмотря на небольшой наклон траектории болида. При расчетах мы полагали, что вектор скорости наклонен всего 3⁰ к линии горизонта. Здесь следует отметить, что увеличение этого угла при неизменных значениях других величин, приводило, как правило, к увеличению значения эксцентриситета и наклона орбиты.

Заключение

Проведенные вычисления показывают, что тунгусское тело до своего входа в атмосферу Земли могло двигаться по орбите близкой к орбите астероида Apophis. Это, в свою очередь, дает оценку частоты появлений таких астероидов в окрестности Земли и позволяет говорить о достаточно частых сближениях астероидов типа Apophis с Землей и их падениях на Землю. Однако проведенные вычисления не исключают кометной природы тунгусского тела, поскольку в случае небольших размеров тела (100 метров и менее в диаметре), гелиоцентрическая орбита имеет большие значения эксцентриситета и наклона практически при всех значениях наклона траектории болида в атмосфере Земли.

Литература.

Васильев Н.В. Тунгусский метеорит. Космический феномен лета 1908 г.// М.: НП ИД «Русская панорама», 2004. – 372 с.

Гольдин В.Д. Об интерпретации некоторых геофизических явлений, сопровождавших падение Тунгусского метеорита. / Космическое вещество и Земля .// Новосибирск: Наука, 1986. – С. 44 – 62.

Кулик Л.А. К вопросу о месте падения Тунгусского метеорита 1908 г. // Доклады АН СССР. Сер. А. 1927, № 23. С. 399-402.

Медведев Ю.Д. Был ли тунгусский метеорит временным спутником Земли? / Тезисы докладов всероссийской конференции «Проблемы небесной механики», Санкт-Петербург. Под ред. А.Г.Сокольского, А.С. Баранова. // СПб.: Изд-во ИТА РАН, 1997. С. 120-121.

Бывшев М.С., Ю.Д. Медведев Вычисление движения небесного тела в атмосфере Земли. / Тезисы докладов всероссийской конференции "Компьютерные методы небесной механики-97", Санкт-Петербург. Под ред. А.Г. Сокольского. // СПб.: Изд-во ИТА РАН, 1997. С. 48-49.

Hills J.G., M.P.Goda The fragmentation of small asteroids in the atmosphere. // Astronomical Journal, 1993. Vol. 105, No. 3. P. 1114-1144.

Войти в систему

I. ОРБИТА И ТРАЕКТОРИЯ