Одним из основных фактов в районе Тунгусской катастрофы 1908 г. является радиальный вывал леса (рис. 1) с общей площадью области поваленных деревьев около 2000 км2 [84, 88] и средним радиусом этой области 25 км. Вывал леса на такой огромной площади могла произвести только воздушная волна. Причем проекция на земную поверхность воздушной ударной волны, которая произвела радиальный вывал леса, должна иметь цилиндрическую симметрию.
По мнению различных авторов, тунгусский радиальный вывал леса могли произвести:
1) взрывная волна [64, 72, 80, 87, 89];
2) баллистическая волна движущегося космического тела [56, 59, 71, 86];
3) комбинация взрывной и баллистической волн [50, 71, 84].
Ответ на вопрос, какая волна произвела тунгусский вывал леса, имеет принципиальное значение для изучения тунгусской проблемы. Для характеристики волны проведем статистический анализ карты поваленного леса в районе катастрофы 1908 г. (рис. 1). Карта составлена в основном по данным экспедиции 1961 г. Комитета по метеоритам АН СССР [88].
Математически эту задачу можно сформулировать следующим образом. Имеем поле n радиально расположенных векторов (направление поваленного дерева представляем как вектор, направленный от корней дерева), n = 338 (рис. 1). Нормальное уравнение прямой, проходящей через i-й вектор, имеет вид (рис. 2):
aix + biy + li = 0, i = 1, 2, 3, .. n, (2)
ai = + cos ai, bi = - sin ai,
li = Ri sin (αi - υi),
где ai — азимут вектора (от северного направления), υ — азимут точки приложения вектора, Ri — расстояние до вектора от начала координат в км, li — расстояние до прямой от произвольного начала координат в км. Подставляя в систему условных уравнений (2) координаты искомого центра совокупности п векторов xk, yk, получим систему невязок ri: ri = ai
xk + bi yk + li, i =1, 2, 3, . . ., n. (3)
Геометрический смысл невязок состоит в том, что ri есть линейное отклонение направления поваленного дерева от общего центра совокупности всех векторов (рис. 2).
Требуя минимум суммы квадратов всех невязок ri, общеизвестным методом наименьших квадратов [102] найдем искомые координаты центра совокупности всех векторов xk, yk. Относительно первоначально выбранной произвольной системы координат: xk = - 0,05 км, yk = - 0,44 км. Для перевода координат xk, yk в географические координаты φ и λ использована привязка выбранного для расчетов начала координат x0, y0 относительно астрономического пункта горы Фаррингтон с известными координатами [38]: φ = 60°54'58", 98; λ = 101°56'59", 70.
Относительно горы Фаррингтон центр совокупности векторов имеет следующие координаты (ось Y направлена по магнитному меридиану): х׳k = -1,55 км; у׳k = -3,4 км.
Учитывая магнитное склонение в 1961 г. в районе Тунгусской катастрофы D≈1,5° [103] и имея в виду, что одной минуте по меридиану соответствует 1852 м, а по параллели — 1852 cos φ м, для центра совокупности векторов получаем следующие координаты:
φ = 60°53'11"; λ = 101°55'11". (4)
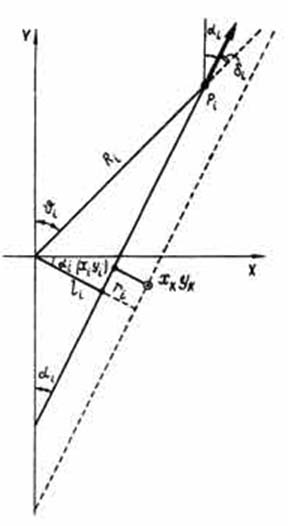 Рис. 2. Изображение поваленного дерева как вектора для обработки карты поваленного леса
Рис. 2. Изображение поваленного дерева как вектора для обработки карты поваленного леса
Среднее квадратичное отклонение направлений поваленных деревьев σ(ri) от найденного центра совокупности векторов равно 2,5 км, что на целый порядок меньше среднего радиуса зоны вывала леса <R>= 25 км. Радиальный характер вывала леса с малыми размерами области рассеяния направлений поваленных деревьев σ(ri) << <R> говорит о том, что ударная воздушная волна, которая произвела разрушения в тайге, имела практически единый центр.
Наличие стоячего леса, сохранившегося на корню после катастрофы и расположенного внутри области радиально поваленного леса [38], исключает наземный взрыв и говорит о том, что центр ударной волны, которая произвела вывал леса, находился в воздухе на некоторой высоте от поверхности земли, не менее 5 км [64]. К таким выводам пришли многие авторы [59, 64, 69,71, 80, 86, 88], но дальнейший анализ фактов и изучение следствий из этих выводов до сих пор еще не были сделаны, в связи с чем в настоящее время нет единого мнения по этому вопросу и продолжаются споры о том, какая волна произвела радиальный вывал. :
Радиальный вывал леса могла произвести:
1) сферическая взрывная волна;
2) баллистическая волна на далеком расстоянии от траектории наклонно двигавшегося тела;
3) баллистическая волна вертикально двигавшегося тела.
Однако малый угол наклона траектории Тунгусского космического тела к земной поверхности (β = 5—17° [38]) исключает для естественного тела образование вертикально расположенной баллистической волны. Остаются две возможности.
По этому поводу выдвигаются разные варианты механизма взрыва космического тела. Одни исследователи [72] считают, что произошло быстрое взрывообразное механическое разрушение космического тела от внутренних перенапряжений при входе тела в плотные слои атмосферы с большой космической скоростью. При этом происходят резкое увеличение поверхности и резкое торможение космического тела. В процессе торможения кинетическая энергия движущегося космического тела переходит в энергию ударной волны, которая при резком и быстром торможении может оказаться близкой к сферической.
Другие исследователи полагают, что быстрый переход кинетической энергии в энергию сферической ударной волны произошел при быстром взрывообразном испарении космического тела (например, ледяного), двигавшегося с большой космической скоростью — около 30 км/сек [69, 80].
Некоторые исследователи считают, что Тунгусское космическое тело представляло собой облако космической пыли или рой частиц [74, 86]:
«На границе тропосферы сопротивление, которое испытывало метеорное тело (рой частиц), резко возросло. Вследствие этого произошло резкое торможение, и высвобожденная кинетическая энергия перешла в энергию взрыва» [86, стр. 121].
По мнению Томской группы, произошел как бы удар облака космической пыли о плотные слои атмосферы, т. е. быстрый переход кинетической энергии в энергию ударной волны произошел при резком торможении облака космической пыли при входе с большой космической скоростью в плотные слои атмосферы. При этом баллистическая ударная волна могла выравняться в сферическую.
По-видимому, здесь нецелесообразно рассматривать, какой из этих вариантов механизма взрыва космического тела является правильным. Возьмем главное и общее содержание из всех рассуждений: при входе в плотные слои атмосферы на сравнительно небольшой высоте в пределах тропосферы в конце своего пути Тунгусское космическое тело претерпело взрывообразное явление с образованием сферической ударной волны, которая произвела радиальный вывал леса в тайге. Причем взрывоподобное превращение должно быть кратковременным и малопротяженным в пространстве, так как при малом наклоне полета космического тела только малопротяженный «взрыв» может обеспечить сферическую ударную волну и радиальный вывал леса. Конечно, такой общей формулировке без всяких ограничений удовлетворяют все виды взрыва космического тела за счет его внутренней энергии.
Сделанное обобщение о взрыве космического тела вытекает из объективного факта — радиальности вывала леса. И действительно, при малом наклоне полета космического тела только сферическая волна может дать на земную поверхность проекцию с цилиндрической симметрией и обеспечить радиальный вывал леса. Баллистическая волна движущегося тела при малом наклоне траектории должна дать проекцию с осевой симметрией, поэтому радиальный вывал в этих условиях она принципиально произвести не может.
Однако некоторые авторы настаивают на том, что радиальный вывал леса в тайге могла произвести баллистическая волна двигавшегося тела, которая могла выравняться в сферическую. В связи с этим рассмотрим возможность выравнивания баллистической волны в сферическую в условиях Тунгусской катастрофы.
Для оценки взрывных явлений и ударных волн, по-видимому, целесообразно отвлечься от точки зрения различных исследователей и рассматривать эти вопросы независимо от механизма и причины образования ударных волн.
Независимо от характера и механизма взрыва космического тела очевидно, что, прежде чем взорваться, тело должно долететь до точки взрыва. Отсюда следует, что в любом случае к моменту взрыва (или «выравнивания») баллистическая волна уже сформировалась. Если ее мощность была достаточной для вывала леса, то она должна была его произвести. В этом случае при малом наклоне полета тела длина активного участка траектории L с точки зрения разрушения баллистической волной должна быть сравнима с областью вывала леса, т. е. L должна быть не менее 25—30 км (рис. 1).
Известно, что баллистическую волну, образовавшуюся при полете тела в атмосфере с космической скоростью, можно считать цилиндрической, а ее движение можно рассматривать по законам цилиндрического взрыва [104].
Таким образом, независимо от природы космического тела к моменту его взрыва над областью разрушений в тайге вдоль траектории этого тела существовала цилиндрическая ударная; волна, эквивалентная по своему действию взрыву цилиндрического заряда.
Из экспериментальных данных известно, что выравнивание ударной волны взрыва цилиндрического заряда конечных размеров происходит на расстоянии, в несколько раз превышающем линейные размеры заряда. В тунгусском случае при длине конечного активного участка траектории космического тела L = 25—30 км, что соответствует длине эквивалентного цилиндрического взрыва при малом наклоне траектории (β = 5—17° [38]) при высоте полета на конечном участке 5— 10 км; выравнивание баллистической волны и ее действие, подобное сферической волне, в пределах области разрушений невозможно, так как выравнивание баллистической волны в сферическую в этом случае можно ожидать на расстоянии не менее 100 км от траектории.
Из всего сказанного можно сделать вывод, что в условиях Тунгусской катастрофы (малый наклон траектории, малая высота полета на конечном участке по сравнению с областью разрушений и др.) радиальный вывал леса был произведен взрывной сферической волной. В данном случае проекция баллистической волны на земную поверхность на конечном участке пути может иметь только осевую симметрию, поэтому необходимым условием вывала леса баллистической волной должно быть наличие осесимметрического относительно траектории полосового вывала леса, что не наблюдается в действительности (рис. 1). Вывал леса взрывной волной признается сейчас многими исследователями; большинство из них указывают на преобладающее действие взрывной волны [80], допуская, таким образом, частичный вывал и баллистической волной.
Поскольку оценка участия баллистической волны в разрушениях имеет большое значение для определения мощности баллистической волны, рассмотрим этот вопрос на фактическом материале. Если мощность баллистической волны была достаточной для вывала леса, то, как уже было сказано, она должна произвести полосовой осесимметрический вывал леса. Причем эта полоса должна пересекать всю область разрушений вдоль траектории от края вывала леса до эпицентра. Поскольку ударная волна валит дерево перпендикулярно своему фронту, а фронт баллистической волны в момент взрыва проходит через эпицентр, при вывале леса баллистической волной должны выполняться следующие условия.
1. Должны существовать углы отклонения δ направлений поваленных деревьев от направления на эпицентр, близкие к 90° (рис.3).
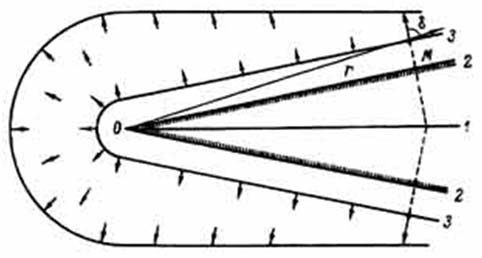
Рис. 3. Упрощенная схема вывала леса баллистической волной при малых наклоне и высоте полета космического тела: 1 - проекция траектории космического тела; 2 - проекция баллистической волны в момент взрыва; 3 – проекция баллистической волны после взрыва; 0 – эпицентр взрыва; r = 0М – линейное отклонение направления поваленного дерева от эпицентра; δ – угловое отклонение направления поваленного дерева от эпицентра
2. На периферии области разрушений должны существовать линейные отклонения r направлений поваленных деревьев от эпицентра, сравнимые с радиусом области разрушений, r = 25—30 км (рис. 3).
Первое условие является необходимым условием вывала леса баллистической волной при малом наклоне траектории и малой высоте полета космического тела. Рассмотрим, как выполняются эти условия для тунгусского вывала леса.
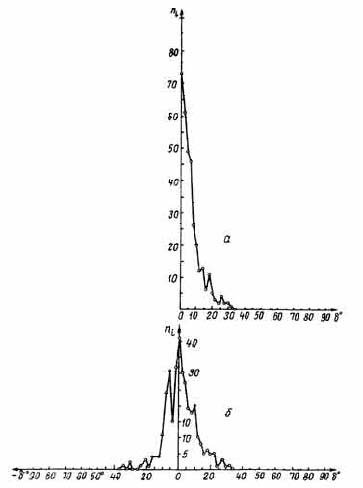
Рис. 4. Распределение угла отклонения δ направлений поваленных деревьев от центра разрушений в районе Тунгусской катастрофы 1908 г. (б). Интервал группирования Δδ = 2°, а – распределение абсолютного значения δ
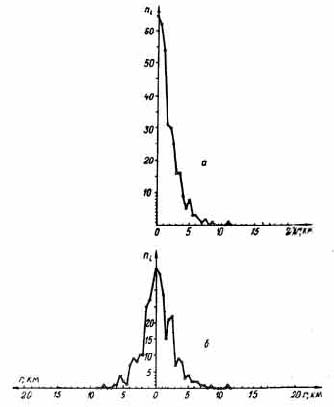
Рис. 5. Распределение линейного отклонения r направлений поваленных деревьев от центра разрушений в районе Тунгусской катастрофы 1908 г. (б). Интервал группирования Δr = 0,5 км, а – распределение абсолютного значения r
Из рис. 4 и 5 следует, что из всей совокупности поваленных деревьев, показанных на рис. 1, нет ни одного с углом отклонения от эпицентра, превышающим 33°, при среднем угле отклонения = 7,5°, т. е. δ<<90°, и нет ни одного с линейным отклонением от эпицентра, превышающим 10 км, при среднем отклонении =1,9 км, т. е. r ≤ 30 км. Эти данные свидетельствуют о том, что оба условия вывала леса баллистической волной в рассматриваемом случае не выполняются, следовательно, при Тунгусской катастрофе баллистическая волна вывала леса не производила.
Таким образом, на основании анализа карты поваленного леса (рис. 1) можно сделать вывод, что в районе Тунгусской катастрофы 1908 г. баллистическая волна двигавшегося космического тела вывала леса не произвела, она не повалила ни одного дерева; вывал леса в тайге был произведен только взрывной сферической волной. Мощность баллистической волны была меньше мощности взрывной волны и была недостаточной, чтобы произвести вывал леса.
Итак, в районе Тунгусской катастрофы 1908 г. произошел взрыв космического тела в воздухе, который и произвел разрушения в тайге.
