Для определения скорости космического тела дополнительно к уравнениям (5) — (8), (11) — (13) и (14) используем независимое соотношение
Sin α = c/v (29)
где α — угол между траекторией и фронтом баллистической волны космического тела (рис. 23); с — скорость баллистической волны; v — скорость космического тела.
Однако, чтобы использовать эту формулу для определения v, нужно знать скорость и направление движения фронта баллистической волны (или угол α). Эти параметры (с и α) можно определить по углам отклонения фронтов взрывной и баллистической волн в результате их взаимодействия. Как уже было показано в § 12, взаимодействие и пересечение взрывной и баллистической волн произошли на симметрично расположенных участках 4 и 5 (рис. 23), которые можно принять за «крылья» баллистической волны. Анализ направлений поваленных деревьев показал, что и на участках 4 и 5 (рис. 23), так же как и во всей области разрушений, вывал леса произвела взрывная волна, но под действием баллистической волны на этих участках взрывная волна изменила свое первоначальное направление.
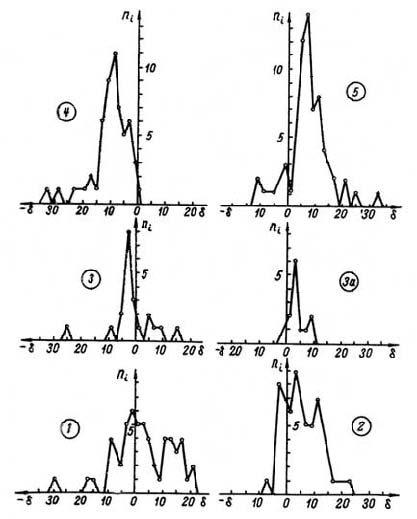Рис. 25. Угловые отклонения направлений поваленных деревьев от эпицентра для различных участков области поваленного леса. Номера участков (1-5) соответствуют обозначениям на рис. 22
На основе статистического анализа направлений всех поваленных деревьев установлено, что линейное отклонение векторов от эпицентра в зонах 4 и 5 (рис. 23) является систематическим и выходит далеко за пределы средней квадратичной ошибки, которая определяется эллипсом рассеяния с полуосями 1,1 и 1,35 км. Анализ карты поваленного леса свидетельствует о том, что угловые отклонения векторов в зонах 4 и 5 также являются систематическими и выходят за пределы средней квадратичной ошибки (рис. 25). Средний угол систематического отклонения векторов от эпицентра в зонах 4 и 5 равен 8°, тогда как среднее квадратичное отклонение в невозмущенной зоне (секторы 19—36, 1—5) равно ±7°.
Отклонение направлений движения ударных волн при пересечении происходит по законам отражения волн от плоскости, проходящей внутри угла ψ между первоначальными направлениями ударных волн (рис. 26). Причем углы «отражения» ударных волн от «плоскости» ψ1 и ψ2 = ψ - ψ1 обратно пропорциональны их интенсивности, поэтому по углу ω ≈ 2ψ1 отклонения направления движения взрывной волны в точках пересечения с фронтом баллистической волны можно оценить количественное соотношение интенсивности взрывной и баллистической волн [115]:
ΔРσ/ ΔРB = ψ1/(ψ - ψ1) = ψ1 /ψ2 (30)
Поскольку после тунгусского взрыва произошло пересечение в пространстве взрывной и баллистической волн, в принципе можно определить положение линии пересечения этих волн на поверхности земли. В первом приближении эта линия соответствует границе между зонами / и 4 и зонами 2 и 5 (линии ОР и OQ, рис. 23). Средний угол отклонения направления поваленных деревьев от эпицентра в зонах 4 и 5 в окрестности линий пересечения ударных волн ОР и OQ равен 8°. Тогда для определения соотношения избыточных давлений на фронтах ударных волн в точке Р пересечения, согласно формуле (30), необходимо определить угол α и первоначальное направление движения баллистической волны.
Совокупность точек пересечения взрывной и баллистической волн (линия ОР и OQ, рис. 23) является совокупностью точек
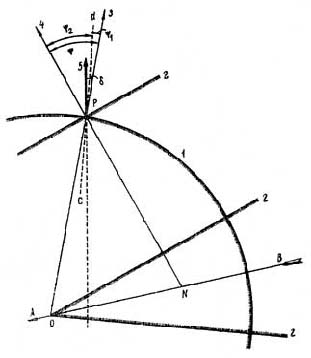Рис. 26. Схема пересечения ударных волн. АВ – траектория космического тела; Р – точка пересечения ударных волн: 1 – фронт взрывной волны; 2 – фронт баллистической волны; 3 – направление движения взрывной волны; 4 - направление движения баллистической волны; 5 - направление движения взрывной волны после пересечения с баллистической волной (направление поваленного дерева) одновременного прихода обеих волн в эти точки.
Отсюда для точки Р имеем
tσ = tT + tB (31)
где tσ — время движения баллистической волны от траектории (из точки N') до точки Р; tT — время движения космического тела из точки N' до точки взрыва О'; tB — время движения взрывной волны из точки взрыва О' до точки- Р. Определение времени движения ударной волны на известное расстояние при известных параметрах волны является решенной задачей для всех типов волн [104]. Время движения взрывной волны tB на расстояние r2 определяется по формулам (5) — (8) и (32) — (33) [104]:
tB = 
1 tB , t0 = r0 (<p1>/<P1>)1/2
где 1 — безразмерное время (6); t0 — динамическое время для сферического взрыва; r0 — динамическая длина сферического взрыва в метрах (8); <p1> и <P1> —средние значения плотности и давления нижнего, слоя атмосферы толщиной, равной высоте взрыва Но.
Время движения баллистической волны tσ на расстояние r2 определяется по формулам (11) — (13) и (34) — (36) [104]:
2 = R2 
-1/2 - ((R/2)1/2/(a2))1/2 + 0,25, (34)
tσ = 2 t0' (35)
t0' = r0' (<p1>/<P1>)1/2 (36)
где 2 — безразмерное время (34); t'o —динамическое время для цилиндрического взрыва; r'0 — динамическая длина цилиндрического взрыва в метрах (13); <p1> и <P1> — средние значения плотности и давления нижнего слоя атмосферы толщиной, равной средней высоте h полета космического тела над областью разрушений. Остальные обозначения в формуле (34) соответствуют обозначениям в формулах (11) — (13).
Тогда для конкретной точки Р, расположенной в окрестности линии пересечения ударных волн на расстоянии 25 км от эпицентра, по известному углу отклонения (ω = δ = 8°) взрывной ударной волны от своего первоначального направления методом последовательных приближений по формулам (5) — (8), (11) — (13), (34), (30) и условию (10), используя соотношение между углом α и скоростью космического тела v (29), можно определить время движения взрывной и баллистической волн в точку Р, угол α и первоначальное направление движения баллистической волны, соотношение избыточных давлений на фронтах взрывной и баллистической волн в точке Р, а также время движения и скорость космического тела на конечном участке траектории.
Скорость космического тела рассчитывалась методом последовательных приближений (табл. 6) по следующей схеме:
1. Выбираем точку Р, расположенную в окрестности линии пересечения взрывной и баллистической волн на расстоянии 25 км от эпицентра взрыва (рис. 23).
2. На этом расстоянии, равном среднему радиусу области вывала леса, избыточное давление на фронте взрывной волны известно: ΔРВ = 0,06± 1 кг/см2 (давление на границе области вывала леса — экспериментальные данные по крупным взрывам [105, 106, 109]).
3. Принимаем высоту взрыва H0 = 7 км.
4. Средняя высота полета космического тела над областью разрушений h = 10 км.
5. По формулам (5) — (8) и условию (10) определяем время движения взрывной волны tB из точки взрыва О' в точку Р.
6. Принимаем, что угол ω = 2ψ1 [115] (рис. 26), тогда при среднем угле отклонения поваленных деревьев от эпицентра (в окрестности линии пересечения ударных волн), равном 8°, угол ψ1=4o.
7. Для начала расчета в первом приближении принимаем скорость космического тела равной 30 км/сек — входные данные. В принципе можно принять большую скорость, например v = 50—60 км/сек.
8. По формуле (20) вычисляем угол α=1°, который определяет положение фронта баллистической волны и направление ее движения.
9. По известному направлению движения баллистической волны и взрывной волны (из эпицентра в точку Р) определяем угол ψ между этими направлениями.
10. По известному ψ и ψ1определяем угол ψ2 = ψ — ψ1.
11. По известным углам ψ1 и ψ2 по формуле (30) определяем избыточное давление на фронте баллистической волны ΔРσ, которое необходимо, чтобы при этих условиях в точке Р изменить первоначальное направление движения взрывной волны на 8°.
12. По известному избыточному давлению и известному расстоянию по формулам (11) — (13) и (34) — (36) определяем время движения баллистической волны tσ от точки N'1 на траектории (пересечение с траекторией перпендикуляра из точки Р на линию фронта волны) в точку Р (рис. 23).
13. По разности времени движения взрывной и баллистической волн в точку Р как точку пересечения волн определяем время движения космического тела tт от точки N'1 до точки взрыва О' (точки О' и N' соответствуют положению на траектории тела, а точки О и N соответствуют положению на проекции траектории на поверхности земли).
14. По известному времени tT и известному расстоянию определяем среднюю скорость движения космического тела на участке траектории N'0' = lτ.
15. По известным параметрам баллистической волны в точке Р по формулам (11) —(13) и (34) — (36) однозначно определяются параметры волны во всем пространстве. Поэтому по известному давлению баллистической волны в точке Р по формулам (11) — (13) и (34) — (36) определим положение баллистической волны в пространстве относительно точки N' в момент взрыва, т. е. определим расстояние, на которое распространилась баллистическая волна из точки N' за время tτ движения космического тела из точки N' до точки взрыва О'. По известному расстоянию и времени в свою очередь определим среднюю скорость движения баллистической волны с за время tT.
16. По известной скорости баллистической волны с и скорости космического тела v определяем угол α между фронтом баллистической волны и траекторией.
Таблица 6 Расчетные данные по определению параметров Тунгусского космического тела методом последовательных приближений
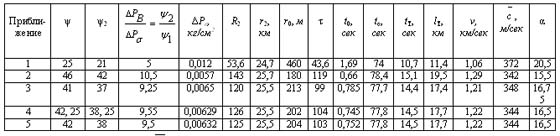
Исходные данные: h=10 км, кг/см2, R=25 км, =0,06 кг/см2, tB=63,3 сек, ψ1=40, v=30 км/сек, α=10.
В результате вычислений, проведенных по пунктам 9—16, мы получили следующее новое приближение скорости космического тела и угла α. По каждому новому приближению скорости космического тела и угла а повторяем операции по пунктам 9—16 до тех пор, пока не получим постоянное значение скорости космического тела: (37)
Здесь следует отметить, что одна из основных формул, по которым рассчитывалась скорость космического тела в табл. 6,— формула (30) является приближенной [115], но в данном случае она с достаточной точностью отражает сущность изучаемого явления.
Чем интенсивнее баллистическая волна, тем на больший угол отклонит она взрывную волну при пересечении. Формула (30) основана на допущении, что при «отражении» ударной волны от плоскости cd (рис. 26) при пересечении ударных волн угол падения равен углу отражения, однако при отражении ударной волны от поверхности угол отражения может быть несколько больше, чем угол падения прямой волны. Точный расчет пересечения неоднородных ударных волн представляет большие математические трудности, но они могут быть проверены экспериментально.
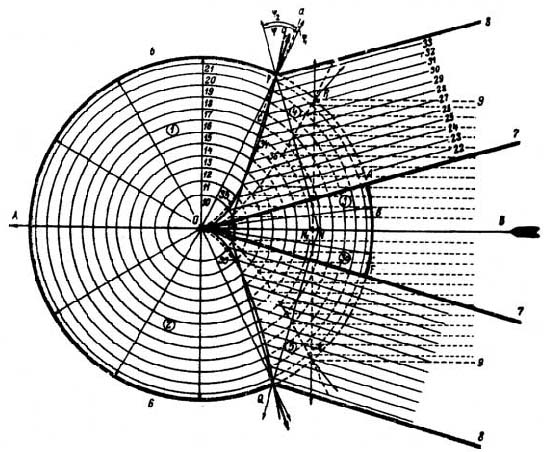
Рис. 27. Схема взаимодействия взрывной и баллистической волн при взрыве Тунгусского космического тела. АВ – направление полета космического тела. 1-3 – области строго радиального вывала леса сферической взрывной волной; 4-5 – области суммарного действия взрывной и баллистической волн; 6 – фронт взрывной волны на среднем радиусе области поваленного леса; 7 – фронт баллистической волны в момент взрыва; 8 - фронт баллистической волны в момент с взрывной ударной волной в точке Р на расстоянии 25 км от эпицентра взрыва; 9 - фронт баллистической волны при скорости космического тела v ≈ 30 км/сек; 10-21 – последовательные положения фронта взрывной ударной волны через каждые 5 сек после взрыва; 22-33 - последовательные положения фронта баллистической волны через каждые 5 сек после взрыва; 34-35 – соответственно расчетная и фактическая линии пересечения взрывной и баллистической волн в последовательные моменты времени; 36 – расчетная линия пересечения взрывной и баллистической волн при скорости космического тела 30 км/сек
Несмотря на приближенность формулы (30), существенно, что в конечном итоге при пересечении с баллистической волной взрывная волна изменит свое первоначальное направление, а после пересечения, когда при всей сложности процесса взаимодействие волн закончится, взрывная волна до самой границы вывала леса будет двигаться и валить деревья по новому измененному направлению. Самое главное, что баллистическая волна оставила заметный след в виде изменения направления вывала леса взрывной волной, по которому можно оценить параметры баллистической волны и космического тела. Если угол «отражения» будет даже в несколько раз отличаться от угла падения взрывной волны (рис. 26), т. е. если угол ψ1 будет значительно больше ω/2, то и в этом случае результат вычисления скорости космического тела существенно не изменится. Более того, предельное значение угла ψ1 ≤ ω = 8° (угол ψ1 физически не может быть больше ω) можно использовать для оценки верхнего значения мощности баллистической волны и скорости космического тела.
Отметим, что проекция конуса баллистической волны в момент взрыва с углом α =16,5° (табл. 6) практически совпадает с зонами 3 и За (рис. 23). Зоны 3 и 3а характерны тем, что, кроме симметричного расположения относительно траектории, в этих зонах сохранился правильный радиальный вывал с очень слабым отклонением от радиальности (рис. 23). Этот факт можно объяснить тем, что внутри конуса баллистической волны ее пересечения с взрывной волной быть не может, а следовательно, не должно быть и сильного отклонения поваленных деревьев от эпицентра.
Схема взаимодействия взрывной и баллистической волн при взрыве Тунгусского космического тела (рис. 27), рассчитанная на основании фактических данных, вполне удовлетворительно согласуется со схемой разрушений в тунгусской тайге (рис. 23), что подтверждает правильность расчетов в табл. 6.
Таким образом, анализ взаимодействия взрывной и баллистической волн при тунгусском взрыве, основанный на фактических данных о вывале леса, показывает, что средняя скорость Тунгусского космического тела на конечном участке траектории длиной около 18 км было порядка 1,2±0,2 км/сек.