До сих пор мы рассматривали главным образом одну особенность разрушений в тунгусской тайге — радиальный характер вывала леса (рис. 1). Как было установлено, вывал леса произвела в основном взрывная сферическая волна. Эту особенность—радиальный характер вывала леса, т. е. действие взрывной сферической волны, — мы будем называть эффектом первого порядка. Однако следует иметь в виду, что взрыв Тунгусского космического тела произошел во время полета. Условия взрыва тела в полете могут внести некоторые искажения сферичности взрывной волны, а следовательно, и радиальности вывала леса. Тунгусское космическое тело, по-видимому, летело со сверхзвуковой скоростью. Поэтому к моменту взрыва над областью разрушений вдоль траектории существовала ударная баллистическая волна. Поскольку баллистическая волна имеет форму, близкую к цилиндрической, при ее взаимодействии с взрывной волной можно ожидать некоторого отклонения взрывной волны от сферической симметрии, отклонения на поверхности земли от цилиндрической симметрии и радиальности вывала леса, т. е. некоторого проявления осевой симметрии области разрушений. Мера отклонения вывала леса от радиальности может служить мерой действия баллистической волны. Если мощность баллистической волны меньше мощности взрывной волны, то разрушения произведет в основном взрывная волна, а баллистическая волна только внесет некоторые искажения в сферическую симметрию взрывной волны. Если мощность баллистической волны больше мощности взрывной волны, то разрушения произведет в основном баллистическая волна, тогда область разрушений будет иметь осевую симметрию, а вывал леса должен быть полосовым.
При Тунгунсской катастрофе взрывная волна произвела в целом радиальный вывал леса, но баллистическая волна, не делая вывал леса, могла произвести искажения сферичности взрывной волны и некоторые отклонения вывала леса от радиальности. Взаимодействие взрывной и баллистической волн и отклонение вывала леса от радиальности мы будем называть эффектом второго порядка.
По эффекту первого порядка (радиальности вывала леса) мы произвели оценку верхних значений параметров баллистической волны и космического тела. По исследованию эффекта второго порядка (отклонение вывала леса от радиальности) можно уточнить оценку параметров баллистической волны и космического тела.
С этой точки зрения сделаем анализ карты поваленного леса (рис. 1). Анализ будем проводить по следующей схеме:
1. Есть ли отклонение вывала леса от радиальности и есть ли проявление осевой симметрии в области разрушений?
2. Если есть, то сделать количественную оценку этих отклонений.
3. По количественной оценке отклонений от радиальности сделать оценку действия баллистической волны и ее параметров.
По параметрам баллистической волны сделать оценку параметров Тунгусского космического тела.
Как показывает рис. 1, отклонение от цилиндрической симметрии области поваленного леса действительно наблюдается. Первое, что довольно четко наблюдается на карте, — это отклонение центра разрушений от геометрического центра области поваленного леса и заметная разница расстояний от центра разрушений (под центром разрушений подразумевается центр совокупности поваленных деревьев как векторов, определенный по методу наименьших квадратов в § 7) до границы вывала леса в различных направлениях (рис. 11).
Рис. 1 и 11 свидетельствуют о том, что в зоне разрушений в пределах азимутов 30—90° и 120—180° четко выделяются два «крыла», симметрично расположенные относительно линии с азимутом 115° (295°). На этих направлениях (максимумы 65 и 165°) расстояние от центра разрушений до границы вывала леса в 2 раза превышает расстояние до границы вывала леса в северо - западном секторе (270—360°) и значительно превышает средний ра диус области вывала леса. Линия АВ является осью симметрии области поваленного леса. Эта линия проходит через центр разрушений, определенный по методу наименьших квадратов в § 7.
Изменение радиуса области поваленного леса в 2 раза не может быть случайным, так как это требует изменения потока энергии ударной волны по различным направлениям в 8 раз. Отсюда следует, что нарушение цилиндрической симметрии вывала леса — достоверный факт. Причина нарушения цилиндрической симметрии "Не случайна еще и потому, что она привела не к произвольному, а к вполне определенному закономерному изменению формы вывала леса с образованием осевой симметрии.
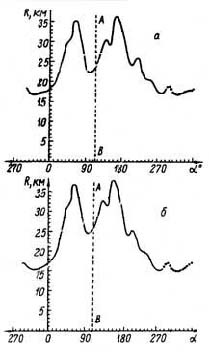Рис. 11. Изменение расстояния от центра разрушений (а) и от эпицентра взрыва (б) до границы вывала леса в зависимости от направления. АВ – линия симметрии
Осевая симметрия области поваленного леса, естественно, отмечается и другими авторами [87], но анализ этого явления до сих пор не был сделан. В работе [72] Г.И. Покровский объясняет асимметрию вывала леса (по данным 1958 г.) направленным действием взрывной волны по раскаленному следу космического тела в воздухе, но такое объяснение не раскрывает причины образования двух симметрично расположенных «крыльев» (рис. 1 и 11). При анализе этой причины необходимо учесть очень важное обстоятельство: нарушение цилиндрической симметрии и образование осевой симметрии области разрушений произошли в общем с сохранением радиальности вывала леса. Следовательно, нарушение цилиндрической симметрии произошло не за счет дополнительной причины вывала леса, а за счет перераспределения энергии взрывной волны. Как было установлено (§ 7), вывал леса во всей области произвела только взрывная волна, но по какой-то причине произошло перераспределение энергии взрывной волны, т. е. возникло ее направленное действие. Таким образом, нарушение цилиндрической симметрии зоны механических разрушений (вывал леса) и эксцентричное расположение в ней эпицентральной области (зона стоячего леса (рис. 1)) говорят о том, что действие ударной волны при взрыве было направленным, причем усиление волны произошло по двум направлениям (азимут 65 и 165°), симметрично расположенным относительно линии АВ (рис. 1).
Проанализируем возможные причины направленного действия взрывной волны. Поскольку протяженность тунгусского взрыва не превышает 4 км, так как σх≈2 км (§ 7), что на порядок меньше зоны разрушений, то причины направленного действия взрывной волны рассмотрим независимо от характера и причины взрыва. В этом случае взрывные явления можно рассматривать по общим законам сферического взрыва, например по законам взрыва обычных ВВ как наиболее изученного.
Причинами направленного действия взрывной волны могут быть:
1) рельеф местности;
2) сильный ветер;
3) форма тела;
4) внешняя оболочка тела.
Анализ показывает, что ни рельеф местности, ни сильный ветер не могут вызвать такую сильную направленность взрывной волны, как при Тунгусской катастрофе, не могут создать два симметрично расположенных направления усиленного действия взрывной волны. Это обстоятельство отмечают и другие авторы [23, 71].
Известно, что взрыв тела произвольной какой бы то ни было формы на расстоянии, в несколько раз превышающем наибольшие размеры тела, создает в однородной неограниченной среде сферическую ударную волну [111]. Поэтому образование направленности действия взрывной волны в тунгусском случае на расстояниях более нескольких километров за счет формы космического тела исключается из рассмотрения.
Таким образом, направленность взрыва Тунгусского космического тела в воздухе на больших расстояних может быть создана только за счет дополнительной оболочки из другого не взорвавшегося вещества. При взрыве тела в воздухе во время сверхзвукового движения оболочкой взрыва могут быть:
1) вещество, входящее в состав самого космического тела;
2) воздух.
Из теории и опытных данных известно, что при взрыве тела в оболочке, создающей направленность взрыва, взрывная волна сравнительно быстро выравнивается в сферическую волну. Направленная взрывная волна выравнивается на расстоянии, в несколько раз превышающем размеры тела и оболочки. Поэтому для создания направленного действия взрывной волны за счет оболочки на расстоянии 25—30 км от центра взрыва необходимо, чтобы размеры оболочки были не менее нескольких километров (2—3 км), а возможно, и более. Но размеры Тунгусского космического тела не могут быть более нескольких десятков метров (§ 10), поэтому оболочка, создавшая направленность взрывной волны, не может входить в состав космического тела.
Как видим, остается только одна причина, создавшая направленность тунгусского взрыва, — воздушная оболочка. При сверхзвуковом движении космического тела со скоростью несколько километров в секунду в воздухе образуется баллистическая волна конической формы. Конус баллистической волны является своеобразной воздушной оболочкой, которая образуется зоной сжатия этой волны. Причем размеры зоны сжатия баллистической волны как оболочки сравнимы с размерами области вывала леса, так как баллистическая волна к моменту взрыва простиралась над всей зоной разрушений. Поэтому по своим размерам баллистическая волна обеспечивает направленность взрывной волны в пределах всей области вывала леса (от эпицентра взрыва до границы вывала леса вдоль траектории).
При взрыве тела в неоднородной атмосфере скорость и поток энергии взрывной волны усиливаются в направлении пониженного давления [104, 112]. При полете тела со сверхзвуковой скоростью впереди тела создается воздушная подушка — уплотнение, сзади — разрежение, в результате при взрыве летящего тела происходит как бы выстрел назад. Конус баллистической волны является как бы огромным жерлом пушки, вдоль оси которого создается некоторая направленность взрыва, что и объясняет эксцентричное положение эпицентра — расстояние от эпицентра до границы вывала вперед по траектории (в общем северо-западный сектор) значительно меньше расстояния до границы вывала назад вдоль траектории. При взрыве летящего тела поток энергии взрыва назад вдоль траектории в несколько раз превышает поток энергии вперед вдоль траектории тела. И действительно, площадь поваленного леса между азимутами 45—225° в несколько раз превышает площадь поваленного леса в секторах 225—360° и 360—45° (рис. 1).
В момент взрыва летящего космического тела создается поток энергии взрыва, направленный назад в разреженное пространство. Однако через определенное время на некотором расстоянии от точки взрыва на траектории давление восстановится до своего первоначального невозмущенного значения. Зона разрежения движется вслед за зоной сжатия баллистической волны, образуя пространственный конус. Этот конус зоны разрежения баллистической волны будет служить волноводом для взрывной волны. По зоне разрежения произойдут некоторое усиление и направленность потока энергии взрывной волны. Проекция этого своеобразного волновода на земную поверхность имеет конусообразную форму. Вдоль проекции образующей конуса по двум направлениям на поверхности земли произойдет усиление действия взрывной волны и увеличение расстояния от эпицентра до границы вывала леса.
Таким образом, баллистическая волна как волновод объясняет существование двух направлений усиленного направленного действия взрывной волны, расположенных симметрично траектории космического тела, что и наблюдается в действительности (рис. 1). При этом очень важно отметить, что собственно баллистическая волна может не производить вывал леса. В данном случае мощность баллистической волны не имеет существенного значения. Здесь важен сам факт существования баллистической волны как волновода для взрывной волны.
По известным формулам [104, 112, 113] в принципе можно решить задачу о том, насколько увеличится поток энергии взрывной волны по зоне разрежения баллистической волны как по волноводу и насколько увеличится радиус зоны поваленного леса по этим направлениям.
Если принять, что давление в зоне разрежения баллистической волны в два раза меньше давления в окружающей невозмущенной среде, что вполне реально [104, 110, 111], то создавшееся усиление потока энергии взрыва вдоль фронта баллистической волны вполне объясняет увеличение радиуса зоны разрушений по этим направлениям и образование «крыльев» области поваленного леса симметрично траектории космического тела. С этой точки зрения ось симметрии области поваленного леса, по-видимому, можно принять за проекцию траектории космического тела.
Создавая зоны усиленного действия взрывной волны, слабая баллистическая волна сама не валит деревья, в зонах усиленного действия продолжает валить деревья только взрывная волна, поэтому слабая баллистическая волна как волновод искажает сферическую симметрию взрывной волны, искажает цилиндрическую симметрию области разрушений и создает осевую симметрию вывала леса, но сохраняет в общем радиальный характер вывала леса, искажается только форма области вывала леса, что и наблюдается в действительности (рис. 1). В этом заключается одна из примечательных особенностей вывала леса в тунгусской тайге (наличие осевой симметрии при общей радиальности вывала леса). Проекция конуса баллистической волны в виде «крыльев» области поваленного леса дает дополнительные данные для оценки параметров баллистической волны и космического тела.
Таким образом, рассматривая причины асимметрии области вывала леса, мы пришли к выводу, что нарушение цилиндрической симметрии и образование осевой симметрии формы области разрушений можно объяснить влиянием баллистической волны на распространение взрывной волны.
Поскольку под действием баллистической волны произошло перераспределение энергии взрыва космического тела по разным направлениям, общую энергию тунгусского взрыва в первом приближении можно считать равной энергии эквивалентного взрыва с радиусом разрушений, равным среднему радиусу области тунгусского вывала леса (§ 8).
Теперь рассмотрим вопрос о влиянии баллистической волны не только на форму, но и на характер вывала леса. Здесь следует учесть, что к моменту взрыва космического тела баллистическая волна была уже сформировавшейся, поэтому нужно рассматривать как факт, что после взрыва тела произошла встреча и пересечение фронтов взрывной и баллистической ударных волн. Известно, что при пересечении двух ударных волн их первоначальное направление меняется [114, 115]. Отсюда следует, что взаимодействие взрывной и баллистической волн при вывале леса должно проявиться в виде отклонения направлений поваленных деревьев от эпицентра, т. е. в виде нарушения цилиндрической симметрии и отклонения вывала леса от строгой радиальности. Следовательно, отклонение от строгой радиальности вывала леса — необходимое условие взаимодействия взрывной и баллистической волн. Мера отклонения от радиальности вывала леса является мерой интенсивности баллистической волны. С увеличением мощности баллистической волны отклонение от радиальности вывала леса должно увеличиваться. Когда мощность баллистической волны увеличится настолько, что она способна будет повалить деревья, произойдет полное нарушение радиальности вывала леса, так как появится полосовой осесимметрический вывал баллистической волной.
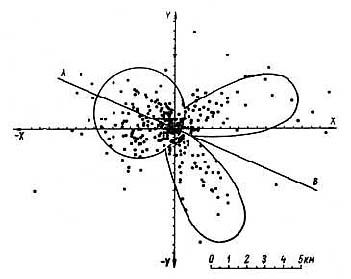Рис. 12. Поле линейных отклонений направлений поваленных деревьев от центра разрушений. АВ – линия симметрии
В тунгусском случае мощность баллистической волны была недостаточной для того, чтобы повалить деревья, но вполне достаточной, чтобы при встрече изменить первоначальное направление взрывной волны.
Проведем анализ совокупности поваленных деревьев как векторов с этой точки зрения. На рис. 12 изображено поле точек пересечения направлений поваленных деревьев с перпендикуляром из центра разрушений, т. е. поле координат хi, yi (рис. 2), отклонений направлений поваленных деревьев от центра совокупности всех векторов (центр разрушений). При вывале леса сферической взрывной волной отклонение направления поваленного дерева от эпицентра является случайной величиной, которая определяется асимметрией корневой системы и кроны дерева, рельефом местности и другими причинами. Исходя из физических условий вывала леса сферической взрывной волной, распределение отклонений поваленных деревьев от эпицентра должно быть близким к нормальному распределению, и при большой площади разрушений оно должно быть симметричным. Однако рис. 12 показывает, что поле координат хi, yi относительно цилиндрической симметрии далеко не симметрично и не равномерно по азимуту.
В общем случае линия осевой симметрии поля случайных точек характеризуется тем, что распределение координат этих точек на оси, перпендикулярной линии симметрии, имеет наименьшую асимметрию. Для поля точек на рис. 12 ось с наименьшей асимметрией имеет направление по азимуту 24°, следовательно, ось симметрии поля точек направлена по азимуту 114°, что с точностью до 1° совпадает с осью симметрии области поваленного леса (рис. 1).
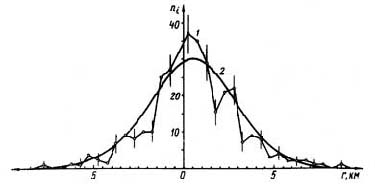Рис. 13. Распределение линейных отклонений направлений поваленных деревьев от центра разрушений: 1 – эмпирическое распределение; 2 - теоретическое
На рис. 13 представлено распределение линейных отклонений направлений поваленных деревьев от центра разрушений (распределение ri; рис. 2) и теоретическое распределение, построенное по числовым значениям моментов, найденных для эмпирического распределения [102, 116].
Начальные моменты распределения вычисляются по формуле [116]
(18)
где хi — значение случайной величины (в нашем случае хi = ri — линейное отклонение направления поваленного дерева от центра совокупности векторов (рис.2)); pi — вероятность данного значения случайной величины хi.
Центральные моменты вычисляются по формуле
(19)
где 
— среднее значение случайной величины.
Эмпирическое распределение имеет следующие характеристики:
1. Среднее значение (1-й начальный момент) v = 0,5 м.
2. Среднее квадратичное отклонение (2-й центральный момент) (μ2 = σ2 = 6,13; σ ~ 2,5 км. Средние квадратичные отклонения по осям координат X и У соответственно равны σx = 2,05 км, σу = 1,65 км.
3. 3-й центральный момент μ3 = 4,1.
4. 4-й центральный момент μ4=170.
5. Асимметрия распределения:
(20)
6. Эксцесс распределения:
(21)
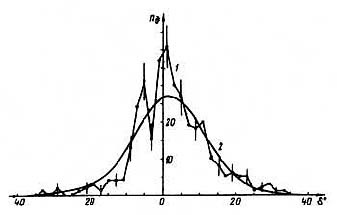Рис. 14. Распределение угловых отклонений направлений поваленных деревьев от центра разрушений: 1 – эмпирическое распределение; 2 - теоретическое
Положительный эксцесс означает, что эмпирическая кривая в центре распределения идет выше кривой нормального распределения.
Аналогично были построены распределения угловых отклонений направлений поваленных деревьев от центра разрушений и распределение координат точек пересечения всех направлений поваленных деревьев между собой (рис. 14 и 15).
Отметим, что большинство вычислений и обработка материалов проведены «вручную», т. е. на обычных счетных машинах. В качестве контроля и ускорения счета вычисления были выполнены также на электронно-счетной машине. Однако определение координат точек пересечения всех векторов между собою и построение распределений этих координат (рис. 15) были выполнены только на машине М-20, так как для построения этих распределений необходимо было определить координаты 56 953 точек пересечений n = 338 векторов.
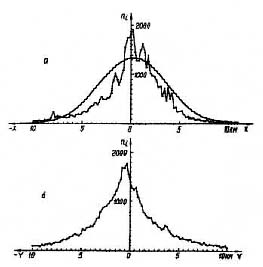Рис. 15. Распределение координат точек пересечения всех направлений поваленных деревьев между собой: а – по оси X; б – по оси Y
Сравнение эмпирических распределений линейных и угловых отклонений векторов от центра с теоретическим нормальным распределением (рис. 13 и 14) показывает, что эмпирические распределения существенно отличаются от нормального. Сравнение по критерию Колмогорова [102] показывает, что эти распределения с вероятностью 0,99 не являются нормальными. Особенно заметно выражена асимметрия распределения координат точек пересечения векторов (рис. 15). Интересно, что асимметрия распределения координаты х точек пересечения векторов (рис. 15, а) значительно больше асимметрии распределения координаты у. Это говорит о том, что нарушение радиальности вывала леса произошло вдоль оси симметрии области разрушений.
При описании области вывала леса в тунгусской тайге в работах [59, 84, 86—89] обычно отмечается, что вывал имеет довольно правильный радиальный характер и что существенных отклонений от радиальности вывала нигде не обнаружено. Но в указанных работах нарушения радиальности вывала рассматриваются с точки зрения отсутствия или наличия полосового осесимметрического вывала леса баллистической волной, т. е. речь идет об эффекте первого порядка. А в данном параграфе рассматриваются отклонения от радиальности в пределах в целом радиального вывала леса взрывной волной, т. е. речь идет об эффекте второго порядка.
Итак, в пределах в общем радиального тунгусского вывала леса наблюдается заметное нарушение строгой цилиндрической симметрии и отклонение от строгой радиальности (рис. 12—15). Однако необходимо выяснить, являются ли эти нарушения радиальности случайными или систематическими. Поскольку совокупность точек пересечения взрывной и баллистической волн в различные моменты времени образует на земной поверхности вполне определенную линию, то, имея в виду взаимодействие взрывной и баллистической волн, область вывала леса можно разделить на две крупные зоны:
1. Зона, в которой взрывная волна валила лес без воздействия, вернее, до воздействия на нее баллистической волны, — зона по одну сторону от линии пересечения ударных волн — северо-западная часть вывала леса.
2. Зона, в которой взрывная волна валила лес после воздействия на нее баллистической волны, — зона по другую сторону от линии пересечения волн — юго-восточная часть вывала леса. Причем обе зоны, каждая в отдельности, имеют общую ось симметрии, точнее, общее направление линии симметрии.
В первой зоне должна выполняться точная радиальность вывала, отклонения от радиальности должны иметь случайный характер, распределение отклонений векторов от эпицентра может быть близким к нормальному и с необходимостью должно быть симметричным. Кроме того, радиальность вывала должна сохраниться в центральной области радиусом не более высоты взрыва, так как в ней относительное действие баллистической волны значительно слабее, чем вне этой зоны
Все нарушения цилиндрической симметрии и радиальности вывала леса должны быть обязаны векторам, расположенным во второй юго-восточной зоне области разрушений. С этой точки зрения сделаем предположение, что общее распределение линейных отклонений r всех векторов от центра разрушений можно представить в виде суммы симметричного распределения, близкого к нормальному, и несимметричного ненормального распределения, асимметрия которого является следствием воздействия баллистической волны. Математически эту задачу можно сформулировать следующим образом.
Имеем асимметричное распределение отклонений n = 338 векторов от эпицентра N(r). Выдвигаем гипотезу, что данное распределение можно представить в виде суммы двух распределений:
N(r) = n(r) + s(r)
где n(r) — нормальное распределение случайной величины (фон, шум); s(r) —распределение систематических отклонений (сигнал), вызванных действием баллистической волны.
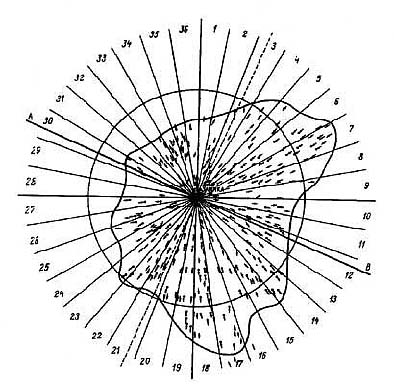Рис. 16. Схема области поваленного леса в районе Тунгусской катастрофы 1908 г. АВ – линия симметрии. Номера секторов (1-16)
Такая гипотеза отвечает реальным условиям тунгусского взрыва. При вывале леса сферической взрывной волной отклонения векторов от эпицентра являются случайной величиной, отклонения векторов под действием баллистической волны являются систематическими. В нашем случае эти отклонения представляют собой сигнал, который мы должны обнаружить и выделить из общего фона случайных отклонений. Если сигнал превышает среднее квадратичное отклонение случайной величины, то его в принципе можно обнаружить и выделить.
Поскольку действие баллистической волны сводится к некоторому изменению направления движения взрывной волны и к изменению направления вывала деревьев, разделим всю область поваленного леса на равные секторы через 10° (рис. 16) и проведем анализ отклонений векторов от центра разрушений по отдельным секторам. Можно ожидать, что по средним отклонениям векторов от эпицентра секторы разделятся на две группы:
1. Секторы, в которых баллистическая волна не действовала, должны иметь меньшие отклонения.
2. Секторы, в которых баллистическая волна действовала, должны иметь большие отклонения.
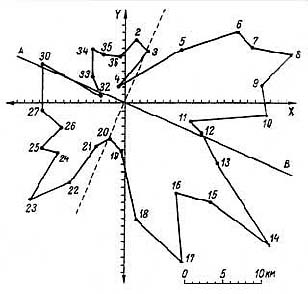Рис. 17. Поле центров пучков направлений поваленных деревьев, распределенных по 36 секторам области разрушений. АВ – ось симметрии; номер сектора (5)
На рис. 17 показана совокупность центров пучков векторов, расположенных в каждом секторе в отдельности. Центр пучка векторов в секторе определялся по методу наименьших квадратов аналогично тому, как определялся центр совокупности всех векторов области поваленного леса (§ 7). Интересно отметить, что контур, проведенный через все центры секторов, в общем напоминает контур области поваленного леса (рис. 1 и 17) (на рис. 17 и последующих рисунках номера секторов 1—36 соответствуют номерам, обозначенным на рис. 16). Отсюда следует, что нарушение асимметрии формы вывала леса и отклонение от радиальности вывала являются следствием одной и той же причины. Ось симметрии совокупности центров секторов в пределах ошибки совпадает с осью симметрии области поваленного леса (рис. 1 и 17). Но самое важное — это то, что действительно существуют группы секторов с большим и малым отклонением собственных центров от центра совокупности всех векторов (начало координат находится в центре поля векторов — центре разрушении).
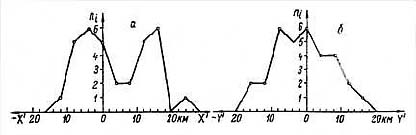
Рис. 18. Распределение координат центров 36 секторов области поваленного леса. По оси симметрии (а); по взаимно перпендикулярной оси (б)
Как и следовало ожидать (рис. 18), распределение координат центров секторов (х'с, у'с) на ось симметрии X' имеет гораздо большую асимметрию (рис. 18, а), чем на перпендикулярную ось Y' (рис. 18, б). Рис. 18, а показывает, что вдоль оси симметрии центры пучков по секторам разделились на две группы с малым и большим отклонением от центра разрушений.
Если систематические отклонения превышают среднее квадратичное отклонение случайной величины и если эти систематические отклонения являются причиной асимметрии распределения, то их можно отделить от случайных отклонений следующим методом.
Сделаем выборку координат центров пучков по оси симметрии X' в интервале
(23)
где μ1 (х'с) и σ1 (х'с) — среднее значение и среднее квадратичное отклонение значений координат х'с центров пучков по всем секторам, m1>1, m1 выбирается так, чтобы μ1 + m1σ1 не превышало наибольшего абсолютного значения случайной величины симметричной части распределения
(24)
В этой выборке отсеется часть систематических отклонений, имеющих наибольшие значения. Без них распределение будет более симметрично, соответственно изменяется и среднее значение и среднее квадратичное отклонение. Найдем среднее значение μ2 (х'с) и среднее квадратичное отклонение σ2 (х'с) для выборки (23).
Для распределения с правой асимметрией очевидно, что
μ2 (х'с) < μ1 (х'с) и σ2 (х'с) < σ1 (х'с) (25)
Далее сделаем выборку координат х'с центров пучков в интервале
μ2 (х'с) - m2 σ2 (х'с) 
х'с μ2 (х'с) + m2 σ2 (х'с) (26)
В этой выборке останется еще меньше систематических отклонений, создающих асимметрию распределения. Оставшееся распределение будет еще более симметрично, для него найдем соответствующие среднее значение μ2 (х'с) и среднее квадратичное отклонение σ3 (х'с).
Сделаем выборку координат х'с в интервале
μ3 (х'с) - m3 σ3 (х'с) х'с μ3 (х'с) + m3 σ3 (х'с) (27)
Найдем среднее значение μ4 (х'с) и среднее квадратичное отклонение σ4 (х'с) для выборки (27).
Выборка координат х'с методом последовательных приближений по этой схеме производится до тех пор, пока не будет выполнено условие
μn+1 (х'с) = μn (х'с) = μ = const (28)
с точностью определения среднего значения μ(х'с).
Этот метод разделения случайных и систематических отклонений применим тогда, когда распределение случайных отклонений симметрично относительно своего среднего значения, а систематические отклонения имеют односторонний характер и создают одностороннюю асимметрию суммарного распределения. В нашем случае отклонения деревьев, поваленных сферической взрывной волной, имеют симметричный характер относительно эпицентра, а отклонения поваленных деревьев, вызванные действием баллистической волны на взрывную волну, имеют односторонний характер — они увеличиваются, смещаясь назад вдоль проекции траектории космического тела.
Для примера рассмотрим сектор 7, рис. 16. Здесь взрывная волна двигалась после пересечения с баллистической волной, в результате которого первоначальное направление движения взрывной волны изменилось в сторону уменьшения азимута, движение взрывной волны отклонилось к северу. Соответственно изменились и направления всех поваленных деревьев, вследствие чего сместился центр пучка векторов этого сектора. Все направления поваленных деревьев в секторе проходят мимо эпицентра, их отклонения сместились в одну сторону назад вдоль траектории космического тела, поэтому они должны выделиться из случайных отклонений как систематическое смещение (сигнал). Таким образом, в тунгусском случае применим изложенный метод разделения случайных и систематических отклонений.
Результаты вычислений методом последовательных приближений по системе формул (23) — (28) представлены в табл. 4 и на рис. 19. Табл. 4 и рис. 19 показывают, что действительно существует группа секторов (6—18, рис. 16), координата х'с центров которых имеет одностоооннее положительное отклонение, в 2,5 раза превышающее среднее квадратичое отклонение симметричной части распределения. Интересно отметить, что эти секторы расположены не хаотически по области разрушений, а вполне определенным образом, охватывая всю юго-восточную часть от азимута 50 до 180° и включая в себя «крылья» области поваленного леса. И что самое важное, они расположены симметрично относительно оси симметрии области разрушений (рис. 16).
Таблица 4 Разделение секторов области разрушений со случайными и систематическими линейными отклонениями направлений поваленных деревьев от эпицентра методом последовательных приближений
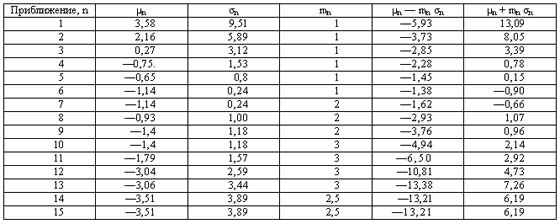
Таким образом, мы получили группу секторов (19—36; 1— 5, рис. 16) с относительно малыми и симметричными отклонениями координат центров от своего среднего значения (рис. 18, в) и группу секторов (6—18, рис. 16), отклонения координат центров которых превышают два средних квадратичных отклонения и являются систематическими отклонениями, вызванными действием баллистической волны.
Рис. 20 наглядно показывает, что действительно центры секторов разделяются на две самостоятельные группы со своими отдельными групповыми центрами, расположенными на оси симметрии области поваленного леса.
По методу наименьших квадратов определим центр совокупности векторов отдельно для обеих групп. Для группы секторов с малыми симметричными отклонениями (1—5; 19— 36, рис. 16, 17) построим распределение отклонений векторов от центра совокупности векторов этой группы. Сравнение эмпирического распределения с теоретическим показывает, что действительно отклонения векторов первой зоны (секторы 1—5; 19—36, рис. 17) от центра подчиняются законам случайной величины и имеют нормальное распределение (рис. 21) со стандартным отклонением σ =1,7 км, следовательно, эти отклонения являются случайными величинами. Относительно большие отклонения векторов второй зоны (секторы 6—18, рис. 16, 17) имеют односторонний систематический характер.
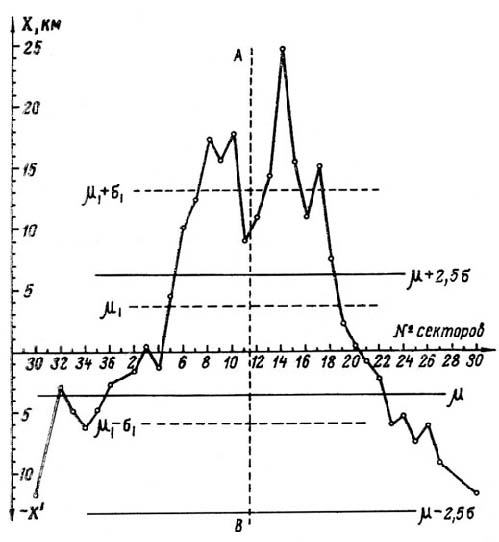
Рис. 19. Изменение координаты центров 36 секторов по оси симметрии области поваленного леса. АВ – ось симметрии
Анализ угловых отклонений векторов приводит к тем же выводам. Угловые отклонения векторов первой северо-западной зоны имеют распределение, близкое к нормальному (рис. 22. а). Отдельные выбросы объясняются наличием локальных полосовых вывалов, как например в секторе 26. Распределение угловых отклонений векторов второй юго-восточной зоны существенно отличается от нормального (рис. 22, 6). Отрицательные отклонения углов δ = α — υ < 0 (рис. 2) являются систематическими отклонениями векторов верхнего правого «крыла» области вывала леса. Положительные отклонения углов δ = α — υ > 0 (рис. 2) являются систематическими отклонениями векторов нижнего левого «крыла» области вывала леса (рис. 16 и 22).
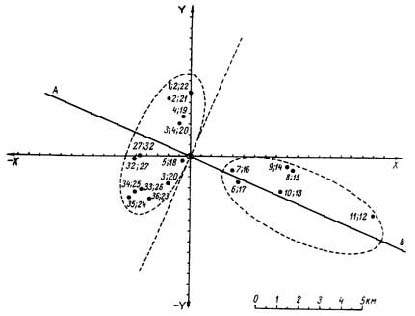Рис. 20. Поле центров пучков секторов, сгруппированных по оси сектора, расположенных симметрично относительно оси симметрии области разрушений. АВ – ось симметрии области поваленного леса. Номер секторов соответствует обозначениям на рис. 16
Таким образом, анализ карты поваленного леса показывает, что, несмотря на общий радиальный характер вывала леса, существуют нарушения цилиндрической симметрии как формы, так и радиальности вывала леса. Эти нарушения являются следствием систематических угловых и линейных отклонений векторов от эпицентра. Гипотеза о том, что асимметричное распределение линейных отклонений векторов состоит из суммы случайных и систематических отклонений (сигнал), полностью подтвердилась, так как среднее значение систематических отклонений значительно превышает стандартное отклонение случайной величины.
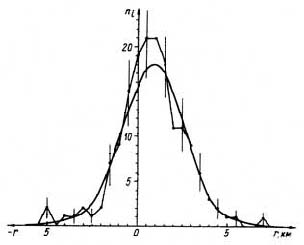Рис. 21. Распределение линейных отклонений направлений поваленных деревьев от эпицентра для зоны невозмущенного действия взрывной волны
Из всего сказанного следует, что действительно в первой северо-западной зоне (секторы 19—36; 1—5, рис. 16) вывал леса был произведен взрывной волной без взаимодействия с баллистической волной. Следовательно, центр совокупности векторов этой зоны является действительным эпицентром взрывной волны. Эпицентр взрывной волны расположен на расстоянии 1,5 км на ЗСЗ от общего центра совокупности всех n = 338 векторов (центр разрушений). Во второй юго-восточной зоне (секторы 6—18, рис. 16) вывал леса был произведен взрывной волной после взаимодействия с баллистической волной. Действие баллистической волны свелось к некоторому изменению направления вывала деревьев, что привело к смещению общего центра векторов от действительного эпицентра назад вдоль проекции траектории. Поэтому для изучения чисто взрывных явлений тунгусского взрыва нужно анализировать
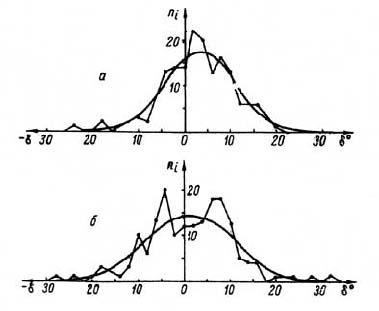Рис. 22. Распределение угловых отклонений направлений поваленных деревьев от эпицентра для различных зон области разрушений. Секторы 1-5; 19-36 (а); секторы 6-18 (б) поле векторов только в первой зоне.
А для изучения действия баллистической волны и определения ее параметров нужно анализировать поле векторов во второй зоне. В первом приближении граница между первой и второй зонами (линия пересечения взрывной и баллистической волн на земной поверхности) проходит по азимуту 50° (между 5 и 6 секторами) и по азимуту 180° (между 18 и 19 секторами, рис. 16).
Для более точного определения линии пересечения ударных волн проведем анализ не по секторам, а по всем векторам в отдельности. Из эпицентра взрыва (центр векторов первой зоны) проведем окружность с радиусом r = 1/2 (σх + σу) = 1,2 км, где σх и σу — средние квадратичные отклонения векторов первой зоны от эпицентра по осям X и У. Эту область в дальнейшем будем называть областью эпицентра. Все поваленные деревья, направления которых проходят через область эпицентра, обозначены кружками (рис. 23). Поваленные деревья, направления которых проходят вне области эпицентра, обозначены стрелками, причем длина стрелки пропорциональна углу отклонения от эпицентра (рис. 23).
Рис. 23 показывает, что зона поваленного леса довольно четко разделяется на участки или области с преобладанием кружков и преобладанием стрелок. Преобладание кружков (60—70%) означает, что цилиндрическая симметрия и точная радиальность вывала леса сохраняются, так как преобладающее количество направлений поваленных деревьев проходит через эпицентр. И наоборот, преобладание стрелок означает, что цилиндрическая симметрия и строгая радиальность вывала леса нарушаются.
По этим признакам зона поваленного леса разделяется на 6 областей, симметрично расположенных относительно линии АВ (рис. 23). В областях 1; 2; 3 и 3а наблюдается четкая картина точного радиального вывала (преобладание кружков, табл. 5), в областях 4 и 5 наблюдается заметное отклонение стрелок от эпицентра. Причем отклонения стрелок в этих областях симметрично расположены относительно линии АВ, которая является осью симметрии всей области разрушений.
Проведенный статистический анализ направлений всех поваленных деревьев показывает, что отклонения векторов от эпицентра в областях 1; 2 и 3 являются случайными. Причем относительное число отклонений (60—70%), не превышающих среднюю квадратичную ошибку, в этих областях удовлетворяет нормальному закону (табл. 5). Отклонение стрелок от эпицентра на участках 4 и 5 (рис. 23) является систематическим и выходит далеко за пределы средней квадратичной ошибки, которая определяется эллипсом отклонений с полуосями 1,1 и 1,35 км. Участки 4 и 5 полностью совпадают с «крыльями» области поваленного леса. В первом приближении границу между участками 1 и 4; 2 и 5 можно рассматривать как линию пересечения взрывной и баллистической волн на земной поверхности.
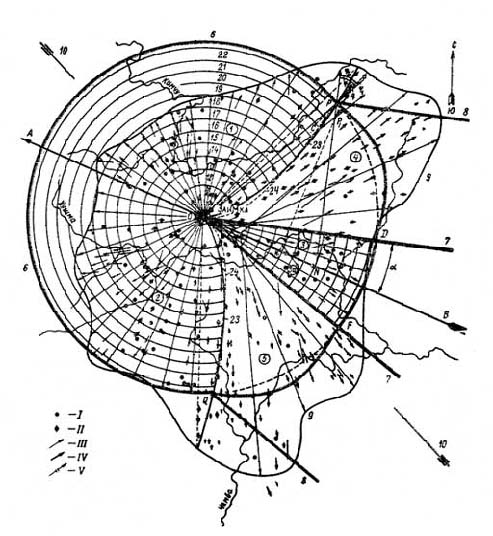
Рис. 23. Схема разрушений в районе Тунгусской катастрофы 1908 г.: 1-3 – области строго радиального вывала леса сферической взрывной волной; 4-5 – области суммарного действия взрывной и баллистической волн; 6 – фронт взрывной волны; 7 – фронт баллистической волны в момент взрыва; 8 - фронт баллистической волны в момент встречи с взрывной волной в точке Р на расстоянии 25 км от эпицентра взрыва; 9 – граница области поваленного леса (по К.П. Флоренскому); 10 – траектория космического тела (по Е.Л. Кринову); 11-22 – последовательные положения взрывной волны через каждые 5 сек после взрыва; 23 – граница между областями со строго радиальным (1, 2) и осесимметричным (4, 5) вывалом леса; 24 – расчетная линия пересечения взрывной и баллистической волн в последовательные моменты времени; I-II – поваленные деревья, направление которых проходит через эпицентр взрыва и соответствует сферической симметрии; III – направления поваленных деревьев, которые отклоняются от эпицентра хаотически; IV - направления поваленных деревьев, которые отклоняются от эпицентра и соответствуют осевой симметрии; V – направление движения ударной волны
Таблица 5 Распределение азимутов поваленных деревьев в районе Тунгусской катастрофы по различным зонам (рис. 22)
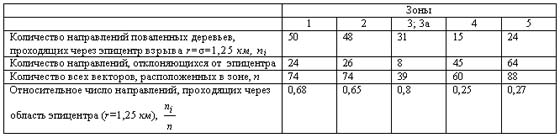
Таким образом, на основе статистического анализа карты разрушений в районе Тунгусской катастрофы дана количественная оценка влияния баллистической волны на вывал леса. По этим данным можно уточнить параметры баллистической волны и космического тела. Отметим, что каждая стрелка на рис. 1 соответствует среднему направлению около 100 поваленных деревьев [88], что обеспечивает надежность результатов обработки карты поваленного леса.