Расчеты в § 10 приводят к интересным рассуждениям. Предполагая, что взрыв космического тела и все разрушения в тайге произошли за счет кинетической энергии двигавшегося тела, по известной мощности баллистической и сферической волн, определенных по фактическим данным, по известной энергии разрушений (в этом случае кинетическая энергия Ек) мы нашли связь между плотностью космического тела и его скоростью (уравнение (15)). Задавая скорость космического тела, по уравнению (15) можно определить минимально возможную плотность тела и, наоборот, задавая плотность космического тела, можно определить максимально возможную в этих условиях скорость тела. И действительно, для каждого значения скорости конкретная величина кинетической энергии строго определяет массу тела (соотношение (1)). Для заданной плотности тела конкретное значение массы строго определяет размеры этого тела. А заданные размеры тела при известной мощности баллистической волны строго определяют скорость этого тела (уравнения (11)—(14)).
Таким образом, система уравнений (11) — (14), (1) и условие (10) при известной кинетической энергии космического тела однозначно определяют основные параметры Тунгусского космического тела: массу, скорость, размеры и плотность. Поэтому, согласно уравнению (15), можно рассчитать максимально возможную скорость в тунгусских условиях для любого тела с заданной плотностью, например для реальных ледяного, каменного и железного тел.
Кривые рис. 8 показывают, что для реальных ледяного, каменного и железного тел (ρт = 1; 3 и 7,8 г/см3) в тунгусском случае при высоте взрыва Н = 7 км скорость не могла быть более 0,6; 2 и 5 км/сек соответственно (рис. 8, 5). Даже при высоте взрыва 10 км скорость этих тел не могла быть больше соответственно 2; 7 и 18 км/сек (рис. 8, 4); если бы эти тела имели большую скорость, то они образовали бы более мощную баллистическую волну и произвели бы полосовой вывал леса, чего не наблюдается в действительности (рис. 1). Но при такой малой скорости взрыв космического тела в воздухе за счет его кинетической энергии невозможен [69, 80]. В связи с этим вопрос о возможности «теплового» взрыва космического тела рассмотрим несколько подробнее.
Под «тепловым взрывом» космического тела будем понимать взрыв тела за счет перехода кинетической энергии в тепловую при резком торможении этого тела. Например, при ударе космического тела о земную поверхность со скоростью 5 км/сек при резкой остановке тело разогреется до нескольких тысяч градусов и мгновенно испарится. Процесс быстрого испарения тела как быстрый переход твердого состояния в газообразное имеет взрывообразный характер, и его можно назвать «тепловым взрывом». Такие взрывы наблюдаются при падении на землю крупных метеоритов со скоростью не менее 3 км/сек [33, 38, 46].
По мнению некоторых авторов, быстрое взрывообразное испарение космического тела, например ледяного, может произойти не только при ударе о землю, но и в воздухе при резком торможении тела в плотных слоях атмосферы. Но для того чтобы обеспечить мощную ударную волну, быстрое взрывообразное испарение тела за 0,1—0,2 сек и мощность процесса испарения, сравнимую с мощностью взрыва пороха, тело должно- двигаться со скоростью около 30 км/сек [69, 80]. Теория и механизм так называемого «теплового» взрыва космического тела в воздухе за счет его кинетической энергии рассмотрены в работах [69, 80]. Необходимым условием «теплового» взрыва в воздухе является большая космическая скорость тела — не менее 30 км/сек [69, 80], что для Тунгусского космического тела до сих пор не подтверждено фактическим материалом. Кроме того, теоретические расчеты процесса разогрева космического тела во время полета в работе [69] основаны на допущении, что на разогрев и испарение космического тела в полете расходуется 0,1—0,01 доли энергии излучения баллистической ударной волны. По замечанию академика Б.П. Константинова, при обсуждении доклада К.П. Станюковича на 10-й метеоритной конференции в июне 1962 г. в Ленинграде в этом расчете не учтен гидродинамический эффект при переносе лучистой энергии от баллистической волны на испаряющуюся поверхность тела, что может изменить результаты расчета на несколько порядков. Таким образом, «тепловой» взрыв космического тела в воздухе не имеет достаточного физического и теоретического обоснования.
Рассмотрим этот вопрос с несколько другой стороны. Рассчитаем энергию и возможные разрушения баллистической волны при условиях гипотетического теплового взрыва, которые не были учтены в работе [69]. Задавая плотность ρт и скорость v космического тела при известной конечной кинетической энергии Ek, по соотношению (1) определяем массу и размеры тела. При известных размерах и скорости по уравнению (14) вычисляется динамическая длина r0, значение которой определяет энергию и параметры баллистической волны во всем пространстве (уравнения (11) — (13)).
В условиях Тунгусской катастрофы длина L активного конечного участка траектории равна около 30 км (рис. 1), протяженность предполагаемого теплового взрыва равна около 6 км [69], поэтому при тепловом взрыве должны быть области разрушений отдельно взрывной и баллистической волнами.
Отметим, что анализ карты разрушений как поля векторов поваленных деревьев показал, что протяженность области взрыва, вернее ее проекция на земную поверхность, вдоль траектории не может быть более 4 км (рис. 4 и 5, § 7). В этом случае еще до взрыва и независимо от его характера при полете со скоростью 30 км/сек космическое тело должно образовать мощную баллистическую волну, которая способна произвести самостоятельные разрушения (табл. 3).
Таблица 3 Основные параметры баллистической волны космического тела в условиях Тунгусской катастрофы при гипотетическом тепловом взрыве
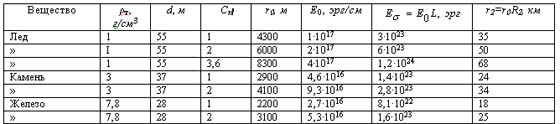
Примечание: mk=8,9·104 т, R2=8,2. Исходные данные: Н0=7 км, h=10 км, 
=0,563 кг/см2, Ek=4·1023 эрг, vk=30 км/сек, ā1=320 м/сек, М=94, 
P
=0,05 кг/см2, L=30 км.
Основные параметры баллистической волны и размеры r2 области вывала леса этой волной при полете в атмосфере со скоростью 30 км/сек космических тел с различной плотностью рассчитаны по формулам (11) — (14) и (1), § 9 и 10. Из табл. 3 видно, что действительно при полете ледяного, каменного и железного тел со скоростью 30 км/сек зона разрушений баллистической волной в тунгусских условиях должна быть сравнима с зоной разрушений взрывной волной.
Рассмотрим этот вопрос в несколько более общем виде. Для космических тел атмосфера Земли является своеобразным фильтром, и не всякое тело не со всякими параметрами может его пройти. В метеоритике хорошо известно, что при падении метеоритов на Землю их кинетическая энергия в основном тратится на преодоление сопротивления воздуха, на образование баллистической волны. Большинство метеоритов расходуют почти всю свою кинетическую энергию, еще не долетая до нижних слоев атмосферы, и теряют скорость на высоте 15—20 км (область задержки), затем достигают Земли при свободном падении под действием силы тяжести [46, 101]. В связи с этим возникает вопрос: может ли обычное космическое тело с реальной плотностью 8 г/см3 долететь до нижних плотных слоев атмосферы (Н0 = 5—10 км), сохранить колоссальный запас кинетической энергии, необходимой для взрыва, пролететь на высоте около 10 км со скоростью около 30 км/сек (!) и не создать мощной баллистической волны, не произвести этой волной никаких разрушений? Возникает и другой вопрос: каким должно быть космическое тело, чтобы, пролетая в атмосфере с огромной скоростью, оно имело большую кинетическую энергию и очень слабую баллистическую волну?
Из аэродинамики известно, что при одних и тех же значениях начальной массы и скорости сопротивление, а следовательно, и мощность баллистической волны зависят от поверхностной плотности, т. е. от количества вещества, приходящегося на единицу площади поперечного сечения тела, а для тел подобной формы, например для шара, мощность баллистической волны в этих условиях зависит от объемной плотности тела. Чем больше плотность, тем меньше размеры тела, тем меньше сопротивление воздуха и мощность баллистической волны. Исходя из таких соображений, Тунгусское космическое тело должно иметь большую плотность, малые размеры и малое сопротивление для того, чтобы оно могло пролететь почти всю толщу атмосферы и сохранить при этом колоссальный запас кинетической энергии, необходимой для взрыва и огромных разрушений в тайге.
Вообще говоря, сохранить большой запас кинетической энергии при полете обычного космического тела в плотных слоях атмосферы с образованием мощной баллистической волны довольно просто. Для этого космическое тело должно иметь большие начальные массу и скорость (так и рассуждают некоторые авторы [87]). Но сохранить в конце пути большую кинетическую энергию и не вызвать мощной баллистической волны при полете с большой космической скоростью — это для космического тела с обычной плотностью (1—8 г/см3) невозможно, так как оно неизбежно должно вызвать мощную баллистическую волну с энергией, сравнимой с запасом его кинетической энергии. Здесь одних условий о большой начальной массе и скорости недостаточно, здесь накладываются дополнительные условия на размеры и плотность космического тела. В тунгусском случае речь идет о большом значении конечной кинетической энергии космического тела при малой доле расхода энергии на образование баллистической волны. Рассмотрим зависимость энергии баллистической волны и размеров разрушений (вывала леса в тайге) этой волной от плотности космического тела. Задавая плотность ρт и конечную скорость vk космического тела при известной конечной кинетической энергии по соотношению (1), определяем конечную массу и размеры тела. Используя уравнение (14), вычисляем динамическую длину r0, по значению которой в соответствии с формулой (13) находим энергию баллистической волны Eσ в зависимости от первоначально заданной плотности космического тела ρт:
, (16)
где L — длина активного участка траектории космического тела, длина эквивалентного цилиндрического взрыва. Используя формулы (11) — (13), (1) и (14), определим размеры области вывала леса rσ баллистической волной в зависимости от плотности космического тела:
. (17)
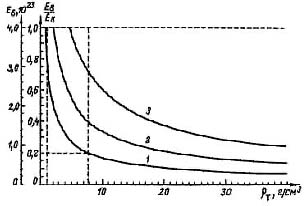Рис. 9. Зависимость энергии баллистической волны и ее отношения к кинетической энергии от плотности космического тела: 1 – CX = 1; 2 – 2; 3 – 3,6
Кривые на рис. 9 и 10 рассчитаны при следующих исходных данных: конечная скорость полета vк = 30 км/сек, конечная кинетическая энергия Eк = 4·1023 эрг, высота взрыва H0 = 7 км, средняя высота полета над областью разрушений h=10 км, длина активного участка траектории L = 30 км. При расчетах сделано допущение, что на коротком участке пути в пределах области разрушений в тайге космическое тело двигалось с постоянными скоростью, массой и размерами. Поскольку начальные масса, размеры и скорость превышают соответствующие конечные параметры тела, то это допущение не меняет существа результатов расчетов.
Космическое тело с реальной плотностью ρт = 1— 8 г/см3, как показывают рис. 9 и 10, пролетая со скоростью 30 км/сек, в тунгусском случае должно образовать баллистическую волну с мощностью, сравнимой с мощностью взрыва, а также должно произвести полосовой вывал леса баллистической волной с шириной полосы вывала, сравнимой с радиусом зоны вывала леса взрывной волной. Одним из важных обстоятельств Тунгусской катастрофы является то, что космическое тело даже в нижних плотных слоях атмосферы непосредственно над областью разрушений пролетело без образования мощной баллистической волны (баллистическая волна не произвела вывал леса даже на ближайшем расстоянии от траектории в конце пути, § 7) и в то же время до конца пути сохранило огромную энергию, выделившуюся при взрыве, который и произвел все разрушения в тайге, т. е. необходимыми условиями тунгусского взрыва являются:
1. Энергия баллистической волны мала по сравнению с энергией взрывной волны: Еσ<<ЕB, Еσ /ЕB ≤1 (§9).
2. Радиус баллистической волны, которая могла бы произвести вывал леса, не должен превышать высоты полета тела: rσ<h или
1.
Таким образом, предположение о том, что тунгусский взрыв произошел за счет кинетической энергии двигавшегося тела, приводит нас к дилемме:
1) либо Тунгусское космическое тело было сверхплотным (ρт ≥ 30 г/см3) и летело с большой скоростью — около 30 км/сек,
2) либо космическое тело имело небольшую плотность (ρт ≤8 г/см3) и летело с малой скоростью — не более 5 км/сек.
Но тогда в первом случае космическое тело не может быть обычным телом с реальной плотностью ρт = 1—8 г/см3, а во втором случае тело может быть обычным, но, имея малую скорость, оно не может взорваться в воздухе за счет кинетической энергии, т. е. мы должны отказаться от предположения, что взрыв тела произошел за счет его кинетической энергии, и считать, что тело взорвалось за счет его внутренней энергии — химической или ядерной. При этом предположении соотношение (1) не имеет места и все вышеизложенные противоречия устраняются.
Рис. 10. Зависимость размеров зоны разрушений баллистической волной и их отношения к радиусу вывала леса взрывной волной от плотности космического тела при гипотетической «тепловом взрыве» этого тела. Исходные данные: H = 7 км, h = 10 км, P1 = 0,563 кг/см2, ā = 320 м/сек, vк = 30 км/сек, Eк = 4 · 1023 эрг: 1 – CX = 1; 2 – 2; 3 – 3,6
В условиях Тунгусской катастрофы, как показывают табл. 3 и рис. 9 и 10, необходимым условием «теплового» взрыва и вообще любого другого типа взрыва космического тела в воздухе за счет его кинетической энергии (при плотности тела ρт ≤ 8 г/см3) является соизмеримость мощности взрывной и баллистической волн ЕB Еσ, соизмеримость зон разрушений взрывной и баллистической волнами , а в связи с этим наличие осесимметрического (относительно траектории) полосового вывала леса, чего не наблюдается в действительности (рис. 1). Из отсутствия полосового осесимметрического вывала леса следует интересный, несколько парадоксальный вывод о том, что с точки зрения «теплового» взрыва космического тела в воздухе «тепловой» взрыв обычного космического тела с плотностью ρт ≤ 8 г/см3 за счет его кинетической энергии в тунгусском случае не возможен.
При взрыве в воздухе обычного космического тела с плотностью ρт = 1—8 г/см3 за счет кинетической энергии при любом механизме взрыва основные разрушения должна сделать баллистическая волна и вывал леса в тайге в этом случае не может быть радиальным.
Таким образом, в тунгусском случае не выполняется ни одно из перечисленных необходимых условий вывала леса баллистической волной, образуемой при полете в атмосфере космического тела с обычной плотностью (ρт≤8 г/см3). Следовательно, Тунгусское космическое тело не могло быть телом с малой плотностью, т. е. не могло быть обычным ледяным, каменным или железным метеоритом, не говоря уже о космической пыли или рое частиц.
Все эти выводы в § 7—11 получены исходя из простого и очевидного факта, что радиальный вывал леса в тунгусской тайге был произведен взрывной сферической волной, а баллистическая волна летевшего космического тела была слабее взрывной волны (условие (10) ). В действительности, баллистическая волна была не просто слабее, а намного слабее взрывной волны.
Однако, несмотря на существенные выводы, сделанные на основании факта радиальности вывала леса, осталась одна неопределенность, которая не позволяет еще более конкретизировать расчеты и выводы,— в уравнение (14) входит произведение размеров и скорости космического тела. Чтобы устранить эту неопределенность, необходимо независимое определение скорости космического тела. Поэтому основной целью дальнейшего анализа должны быть поиски методов независимого определения скорости космического тела на основании достоверного фактического материала.
>