Концепция прогрессивного дробления Тунгусского метеорита, завершившегося взрывом, была впервые высказана в 1958 г. М.А. Цикулиным [382, 383] на основе анализа данных о поле вывала леса, полученных экспедицией АН СССР 1958 года [373]. В работе К.П. Флоренского и его сотрудников [373] впервые было указано, что такое прогрессивное дробление может привести к резкому торможению тела.
Более подробно, хотя и в качественной форме, этот физический механизм рассмотрел в 1966 г. Г.И. Покровский [302]. Он показал, что разрушение тела под действием аэродинамических нагрузок быстро ускоряется по мере его дробления на все более мелкие осколки. Заключительная стадия этого процесса носит лавинный характер и подобна взрыву.
Количественная теория такого дробления была разработана в 1976 г. С.С. Григоряном [103] и усовершенствована им же в 1979 г. [104]. В 1985 г. В.А. Бронштэн [52] обобщил механизм Григоряна на случай одновременного протекания дробления и испарения.
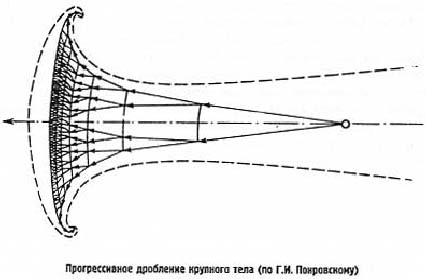Согласно теории Григоряна, разрушение тела будет происходить по сколовому механизму, так как внутри метеорита будут действовать преимущественно сжимающие напряжения, создаваемые перепадом давления на лобовой и тыльной поверхностях тела. Когда давление на лобовой поверхности достигнет разрушающего значения, по телу начнет перемещаться фронт разрушения, а дробленая масса будет растекаться в стороны. Тело будет все уплощаться, а края его, как показал еще Г.И. Покровский [302], отогнутся назад. Процесс завершается практически мгновенным испарением мелких осколков, что эквивалентно сильному взрыву.
Реальная картина разрушающих напряжений под действием аэродинамической и инерциальной нагрузки в метеоритном теле включает и сжатие, и растяжение, и сдвиг, осложненные природными неоднородностями. Теоретически эта задача для шарообразного объекта исследовалась в 1967 г. Ю.И. Фадеенко [351]. Позже, в 1991 г., аналогичные расчеты были проведены с использованием числовых данных, экспериментально определенных для метеоритных пород, в работе В.И. Цветкова и А.Я. Скрипник [381]. При этом выяснилось, что метеориты должны дробиться при относительно небольших скоростных напорах. (На это обстоятельство указывал В.А. Бронштэн в 1981 г. в книге [49] на основании данных наблюдений о дроблении метеоритов в полете.)
Теория Григоряна не привлекла внимания исследователей Тунгусского явления скорее всего из-за ее сложности (в работе [104] 92 формулы, причем большинство - из теории сопротивления материалов). Лишь в 1985-1986 гг. Б.Ю. Левин и В.А. Бронштэн [259, 465] использовали ее для расчета дробления Тунгусского метеорита. В 1994 г. В.А. Бронштэн опубликовал сводку расчетных формул, которые следует применять для вычислений по теории Григоряна [61].
В теории Григоряна выделяются три характерные высоты, определяющие ход процесса дробления: Z1 - высота начала дробления, Z2 - высота, на которой поперечный радиус тела (в направлении, перпендикулярном траектории полета) увеличивается вдвое, и Z3 - высота полного разрушения (взрыва)1.
В работе [61] В.А. Бронштэн исследовал зависимость этих высот от начальных параметров тела и условий его входа в атмосферу. Были получены следующие результаты:
1. Значение Z1 зависит только от прочности 
* вещества тела. В случае цилиндра, летящего ориентированно, Z1 на 8-9 км больше при учете испарения, чем без него.
2. Значение Z2 зависит только от угла наклона (повышаясь при переходе к более пологой траектории на 2-4 км), от прочности (понижаясь с увеличением * в 50 раз на 6-8 км) и особенно от плотности тела (понижаясь при увеличении ее вдвое на 17 км) При учете испарения Z2 заключены в интервале 27-42 км и могут превышать Z2 без испарения на 0,5-20 км (наибольшее различие - для более плотного тела). У более прочного тела различие больше, чем для малопрочного, для цилиндра на 6 км больше, чем для сферы.
3. Значение Z3 слабо зависит от прочности (понижение при тех же условиях на 0,7-1,0 км), сильнее от угла входа (повышение для более пологой траектории на - 4 км) и особенно сильно от плотности тела (повышение ее вдвое снижает значения Z3, на 10-11 км). Для всех вариантов Z3 заключено в пределах 7-15 км.
В 1993 г. были опубликованы (почти одновременно) две работы, в которых предлагались выведенные независимо теории прогрессивного дробления крупных метеоритных тел. Одна из них принадлежит перу американских ученых Дж, Хиллса и М.П. Годы [442], другая - перу их соотечественников К. Чайба, П. Томаса и К. Цанле [423].
Хиллс и Года ничего не знали, к сожалению, о работах С.С. Григоряна, в их статье нет на него ссылок. Но, как показал в 1995 г. В.А. Бронштэн [63], их теория тождественна теории Григоряна. Идя несколько иным путем, они пришли к тем же расчетным формулам, какие вытекают из теории Григоряна и приведены в [61]. В работе Хиллса и Годы приведено множество графиков, выражающих параметры движения и распада крупных тел в зависимости от исходных данных (масса, плотность, скорость и угол входа).
Работа К. Чайба, П. Томаса и К. Цанле [423] была опубликована почти одновременно с работой Хиллса и Годы, и поэтому не содержит ссылок на нее. Но о работе С.С. Григоряна авторы статьи [423] знали и сослались на нее, хотя никак ее не использовали и не обсуждали. Они предложили свою собственную теорию, основанную на следующих соображениях.
Метеорное тело аппроксимируется прямым круговым цилиндром, движущимся в атмосфере вдоль своей оси. Осевое давление убывает вдоль оси цилиндра линейно от некоторого значения ра на лобовой поверхности до почти нулевых значений на тыльной. По мере внедрения тела в более плотные слои атмосферы ра растет экспоненциально, пока не наступит вязкое разрушение. Цилиндр растекается в направлении, трансверсальном к направлению движения. При этом эффективное сечение цилиндра так же экспоненциально растет. Фронт разрушения перемещается от лобовой поверхности к тыльной. Наиболее быстро расширяющиеся элементы цилиндра увлекаются потоком.
Помимо произвольного предположения об ориентированном движении цилиндра, авторы [423] ввели еще несколько предположений. Именно они полагали, что цилиндр, деформируясь, сохраняет цилиндрическую форму, сплющиваясь в продольном направлении и расширяясь в поперечном. Далее, они предположили, что плотность разрушающегося цилиндра остается постоянной.
В этих предположениях Чайба и его коллеги рассчитали движение в атмосфере тел различного состава, массы и начальной скорости и сделали далеко идущие выводы о том, что Тунгусское тело не могло быть ядром или осколком кометы, а имело астероидную природу. Этот их вывод будет подробно рассмотрен в гл. XIV, а пока остановимся на оценке теории.
Теория Чайба-Томаса-Цанле имеет по сравнению с предыдущими ряд слабых сторон. Прежде всего в ней учитывается только гидростатическое равновесие и не учитывается динамика разрушения тела по сколовому механизму. Далее, весьма далеко от реальной действительности предположение о движении тела в направлении оси цилиндра. Выбор цилиндрической формы тела является произвольным. Неясно, как вычисляется высота "взрыва".
Подробная критика работы [423] была выполнена В.А. Бронштэном и И.Т. Зоткиным в начале 1994 г. в статье, представленной тогда же в редакцию журнала Nature, где была опубликована статья [423]. Редакция Nature сперва предложила авторам сократить статью до 700 слов, а когда это было сделано, все же отклонила ее как полемическую. Тогда Бронштэн и Зоткин опубликовали ее в "Астрономическом вестнике" [62]. Интересно, что, представляя в "Астрономический вестник" другую статью, содержащую критическое сравнение всех трех теорий (Григоряна, Хиллса и Годы, Чайба-Томаса-Цанле). В.А. Бронштэн [63] сделал ссылку на статью [62] как находящуюся в печати в Nature, не зная, что она будет отклонена.
Количественное сравнение высот взрыва Тунгусского тела при разных предположениях о его составе, начальной массе и скорости, согласно расчетам по различным теориям (Григоряна, той же теории с поправкой Бронштэна на испарение [52] и Чайба-Томаса-Цанле), было выполнено в работах [62,63]. Оказалось, что вычисления по теории Чайба и др. дают завышенные высоты полного разрушения тела - на несколько километров (до 10-12), что и привело авторов теории к ошибочному заключению о том, что Тунгусское тело не могло быть кометой.
С критикой теории Чайба и его коллег выступили С.С. Григорян и В.А. Бронштэн летом 1995 г. в своих докладах на конференции по Тунгусскому метеориту в Москве, а С.С. Григорян - еще и на конференции летом 1996 г. в Болонье. Но публикация статьи [423] в таком престижном международном журнале как Nature сделала свое дело. Многие исследователи [433, 467, 493, 500] восприняли ее некритически, и в своих работах ссылались на результаты Чайба и его коллег как на заслуживающие доверия.
Но так поступили не все. Примером критического подхода к работе Чайба и др. может служить статья Дж. Лайна и М. Таубера [469], которые выполнили расчеты при более разумных предположениях о форме и коэффициенте сопротивления Тунгусского тела, чем в [423], и получили гораздо более низкие высоты его разрушения, чем Чайба и его коллеги.
В работах [104, 442] движение уже разрушенного тела рассматривалось в жидкостном приближении. На основе этого приближения в работе В.В. Светцова и его соавторов [500] были проведены прямые численные расчеты движения сквозь атмосферу тел размерами 30-100 м. При этом использовались свободно-лагранжева схема и эйлерова схема с отслеживанием контактной границы вещества метеороида с воздухом. Расчеты по обеим схемам дали близкую картину.
Согласно этим расчетам, на начальной стадии разрушения, сразу после перехода от твердого состояния к диспергированному (в рамках жидкой модели), возникают неустойчивости типа Рэлея-Тейлора (в передней части тела) и Кельвина-Гельмгольца (на боковой поверхности). Тело теряет массу за счет сдува его вещества потоком воздуха. При этом оно может не уплощаться, как в схеме Григоряна, а приобретать коническую форму с каверной на тупом носике конуса и с образованием вдоль оси симметрии сквозного канала. Диаметр оболочки тела увеличивается, оно приобретает форму тора и, наконец, разрывается, подобно шрапнели, на мелкие фрагменты. Тем не менее, еще долго облако фрагментов охватывается единой ударной волной.
В работе [500] были приведены высоты разрушения крупных метеороидов по аналитическим моделям Григоряна [104] и Мелоша [473] для двух параметров: а) каменный (
0 = 3 г/см3), v0= 15 км/с; б) ледяной (0= 1 г/см3), v0= 35 км/с. Наклон траектории в обоих случаях был выбран 45°. Второй пример близок предполагаемым параметрам входа в атмосферу Тунгусского метеорита. Если положить начальную массу его равной 2 106 т и плотность 1 г/см3, то по графику работы [500] высота взрыва получится 4 км, а при более пологой траектории - 5-7 км, что хорошо согласуется с другими оценками, как теоретическими, так и сделанными на основе данных по лесоповалу, сейсмике и т. д.
Иная картина получилась при гидродинамическом моделировании. В.В. Светцов и др. [500] рассмотрели вертикальный вход в атмосферу ледяного тела с начальным радиусом 100 м и начальной скоростью 50 км/с (что слишком велико для Тунгусского метеорита). Полный распад такого тела в лагранжевом приближении наступил на высоте около 2 км в случае сферической формы тела или около 5 км при цилиндрической. Эйлерово приближение дало еще меньшие высоты. Однако переход к меньшим размерам, меньшей скорости и более пологой траектории должен "поднять" эти высоты до 7-8 км. В заключении своей работы В.В. Светцов и его коллеги [500] отметили преимущества аналитических методов по сравнению с двумерным численным моделированием, которое требует совершенствования в направлении учета неправильной формы, гидродинамических неустойчивостей и абляции.
Не остался в стороне от расчетов разрушения крупных тел в атмосфере и В.П. Коробейников. В публикации 1992 г., совместно с П.И. Пушкиным, Л.В. Шуршаловым и С.Б. Гусевым [452] он осуществил моделирование механического разрушения тела под действием аэродинамических и массовых сил инерции численным методом конечных элементов. В другой работе 1994 г., совместной с В.И. Власовым и Д.Б. Волковым [220], был применен способ расчета путем разложения в ряды по сферическим функциям. Анализ возможных траекторий входа достаточно крупного космического тела со скоростью от 11 до 72 км/с показал, что могут существовать три типа траекторий: а) пролетная (с возможным рикошетом от атмосферы); б) сближение с торможением и распадом тела; в) сближение и удар о земную поверхность. Этот вывод не содержит, правда, ничего нового и является тривиальным.
В работе [221] В.П. Коробейников, С.Б. Гусев и И.В. Семенов рассмотрели дробление и распад тела путем численного решения уравнений термоупругости методом конечных элементов. Напряженно-деформированное состояние тела предполагалось квазистатическим.
В работах [220, 221, 452] были рассмотрены разные варианты набора параметров Тунгусского тела с начальным радиусом 38 и 45 м, плотностью 0,6 г/см3 и скоростью входа от 23 до 35 км/с. В [220] было рассмотрено также дробление Сихотэ-Алинского железного метеорита и вход и разрушение кометы Шумейкеров-Леви в атмосфере Юпитера.
Это явление, происходившее между 16 и 21 июля 1994 г. и заранее предсказанное астрономами, возбудило всеобщий интерес к проблеме разрушения и распада крупных тел, входящих в атмосферы планет. К сожалению, вход в атмосферу Юпитера всех 21 фрагментов, на которые раздробилась комета под действием приливных ускорений от гигантской планеты, происходил на обратной стороне Юпитера и непосредственно наблюдаться с Земли не мог. Но многие исследователи применили к расчету процесса разрушения этих фрагментов теорию Григоряна (в России) или теорию Чайба-Томаса-Цанле (например, работы [422, 433]).
1 В работах [61, 104] приняты другие обозначения.