Точные вычисления орбит, по которым метеориты двигались до их вхождения в поле тяготения Земли, стали возможными после получения двух фотографий, двух падений каменных метеоритов (найденных). Один из них Pribram, упал в Чехословакии в 1959 г.и был сфотографирован на двух пунктах [1]. Другой метеорит, Logt City упал в Оклахоме в пределах Пре-рийской сети в 1972 г. [2]. Для реального вычисления орбиты надо знать точку падения и иметь «засечки» хорошо работающего метеоритного патруля. И даже это зачастую не может однозначно решить проблему, если траектория полета в атмосфере будет пологой. Но, тем не менее, имеются ряд публикаций [3], где сделаны попытки привязать орбиту Тугнгусского метеорита к метеорному потоку ![]()
А теперь, чтобы понять всю сложность механики полета такого тела и ее неоднозначность, нам надо обратиться к астродинамике, и именно к ее инженерной части, которая существует более 60 лет.
Непременным условием попадания метеорита в Землю является непревышение прицельной дальности эффективного радиуса планеты, т.е. линия, по которой направлена входная планетоцентрическая скорость метеорита, должна проходить на таком расстоянии от Земли, чтобы искривление траектории могли привести к встрече. Причем эффективный радиус тем больше, чем меньше планетоцентрическая скорость входа в сферу действия Земли. Согласно работе [6], мы можем найти эффективный радиус Земли:
где К = 3,986032 103 гравитационный параметр Земли, R=6371 км - радиус Земли, По Портеру [7] скорость спорадических метеоритов 18-24 км/с. Скорость потока Итак, для реальных скоростей мы имеем следующие значения эффективного радиуса.
Спорадические min Рассмотрим рис.6.1, из которого совершенно ясно, что пологая траектория падения возможна только при заходе тела с орбиты типа 3 и в любом случае попадание в сферу эффективного радиуса закончится падением на планету.
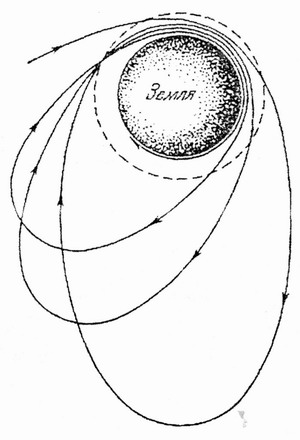
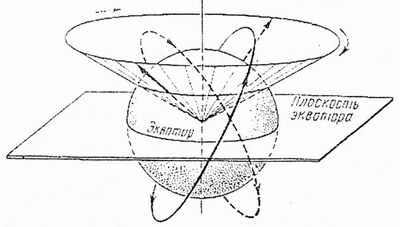
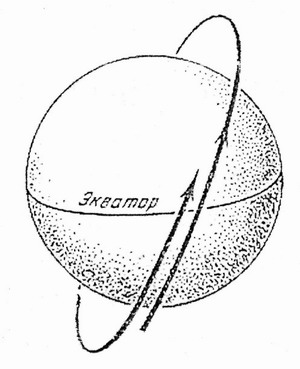
А теперь рассмотрим сферу гравитационного действия Земли. Планетоцентрическая траектория внутри сферы действия Земли - всегда гипербола, поэтому метеорит после входа в сферу действия должен покинуть ее, если не встретит атмосферу или планету (для нашей планеты сфера действия 0,93 млн. км). Могут сложиться условия, когда, потеряв часть скорости от торможения в атмосфере, метеорит превратится в спутник с большой эллиптической орбитой (рис.6.2). Завершив один оборот, он снова войдет в атмосферу, потеряв часть скорости, снова выйдет на эллиптическую орбиту, уже меньшего размера и несколько иначе расположенную. Апогей приблизится к Земле, перигей приблизится очень слабо, а большая ось орбиты повернется на некоторый угол. Большое количество эллипсов гасит гигантскую скорость первоначального входа в атмосферу. Помимо всего, метеорит - спутник будет подвержен прецессии плоскости орбиты (рис.6.3) и смещению восходящего узла за один виток (рис.6.4), что является следствием несферичности Земли.
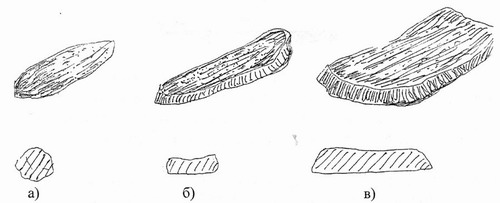
Необходимо упомянуть читателю, что визуально спутник виден при прохождении линии разграничения дня и ночи, а таковыми у спутника могут быть всего несколько витков! [8]. И поэтому, если Тунгусский метеорит и вращался на вытянутых эллиптических орбитах, его никто бы и не увидел. В данной статье не рассматривается аэродинамика полета в плотной атмосфере, но необходимо указать на три вида входа с ближних к Земле орбит по Бекеру [5], рис.6.5. На рис.6.6 приведены три формы метеорита, которые дадут траектории согласно рис.6.5. При попадании высокоскоростного тела в эффективную сферу, траектории могут быть существенно сложней и подчиняется гиперзвуковой аэродинамике и значительно менять углы тангажа. В частности имеется описание падения одного из Алтайских метеоритов (1954 г.), где вертикальное падение обычного хондрита над самой Землей изменило траекторию по тангажу на 90°. Поэтому, исходя из характеристик пологих траектории падения, возникших после схода сильно эллиптических орбит, или при попадании скоростных метеоритов в эффективную сферу Земли, при которых от точки входа до падения десятки тысяч километров ничего нельзя сказать о первичной траектории тела. В данном случае конечная видимая часть траектории ничего не говорит о его орбите.
Литература
Рис. 6.1. Падение метеорита на Землю
Рис.6.2. Падение метеорита по тормозным эллипсам
Рис. 6.3. Прецессия плоскости орбиты метеорита спутник
Рис. 6.4. Смещение восходящего узла за один виток
Рис.6.5. Траектория спуска в атмосфере с близкой к планете орбиты зависит от аэродинамических характеристик метеорита
Рис. 6.6. Форма метеоритов, дающих траектории согласно рис.5, (внешний вид и сечение) аэродинамического качества формы: а) - о; б) - до 0,5; в) - около 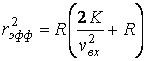
- планетоцентрическая скорость метеорита.
![]()
![]()
=18 км/с
=7499,5 км
=6934,8 км
=6492,3 км
r-R=1128 км r-R=563 км r-R=121,3 км
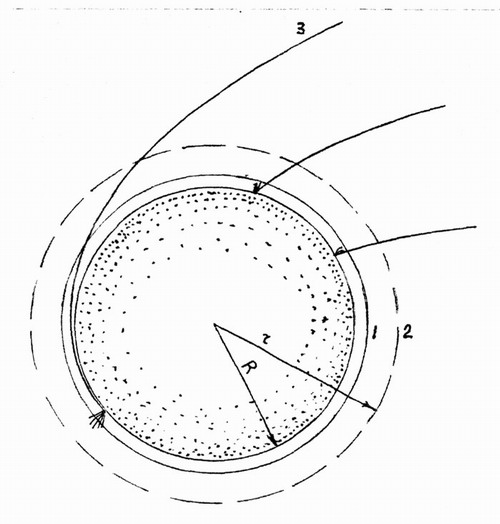
1 - атмосфера, 2 — эффективный радиус, 3 - падение метеорита по пологой траектории, имеющее минимальное тормозное ускорение