А.Г.ИЛЬИН, В.А.ВОРОБЬЕВ, В.В.БАЙЕР, СВЯЗЬ ПАРАМЕТРОВ ПОРАЖЕНИИ BETОK ЛИСТВЕННИЦ СО СВЕТОВОЙ ЭНЕРГИЕЙ
До настоящего времени не было сделано попытки ввести количественную оценку интенсивности поражений, которая непосредственно связана с величиной световой энергии, поглощенной веткой в момент взрыва.Требовалось найти параметры поражений, которые характеризовали бы их интенсивность. Оказалось, что такими параметрами могут служить сектор поражения ε и диаметр d пораженной ветки слоя 1908 года (рис. 1).
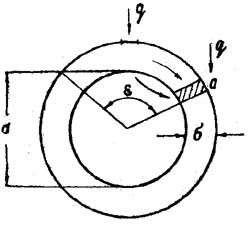Рис. 1. Параметры, характеризующие интенсивность ожога.
Рассмотрим ветку, расположенную в плоскости, касательной к фронту световой волны. Пусть на единичную площадку участка ветки, перпендикулярного световому потоку, падает энергия q кал/cм2 светового излучения. Будем считать, что энергия, падающая на такую же площадку, расположенную на краю поражения (в точке а) под углом ε/2 к световому потоку частично отражается, а поглощенная этим участком энергия полностью расходуется на нагревание коры в этом месте до температуры t, при которой погибает камбий. Эта энергия будет, очевидно, минимальной в пораженном слое. Тогда нетрудно показать, что будет выполняться следующее соотношение:
(1)
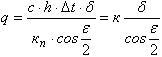
где c – удельная теплоемкость коры, h – удельный вес коры, δ – толщина коры, ∆t = t – t0, t0 – начальная температура коры, кn – коэффициент поглощения к=ch∆t/кn=const для любого участка ветки. Для горизонтальной ветки с произвольным азимутом α имеем:
(2)
где q0 - плотность световой энергии в данной точке, α0 – азимут проекции вектора светового потока на горизонтальную плоскость, φ0 - угол между горизонтальной плоскостью и направлением светового потока.
Из (1) и (2) получаем:
(3)
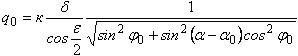
Для ветки, перпендикулярной направлению светового потока
α - α0 = 
/2 или 3/2 и q0 =q.
Таким образом, имеется принципиальная возможность при известных параметрах, стоящих .в правой части выражения (3), вычислить величину плотности световой энергии в данной точке.
В связи с тем, что многие параметры, характеризующие теплофизические свойства коры, пока не известны, ограничимся качественным рассмотрением полученных выражений, принимая, что k = const для всех веток. Азимут α каждой ветки известен, угол ε измеряется на каждом спиле, α0 и φ0 определяются из геометрических соображений. Остается неизвестным параметр δ, так как мы не знаем, какую толщину коры имела ветка на данном участке в 1908 году. Однако эту величину можно получить косвенным путем. Для каждого диаметра живых веток можно найти среднее значение толщины коры и использовать это значение в дальнейших расчетах.
Для выяснения зависимости между диаметром ветки (без коры) и толщиной коры летом 1964 года в районе эпицентра взрыва были исследованы концы живых веток трех лиственниц, растущих в различных условиях.
Лиственница № 1 - у Заимки Кулика, почва сухая, возраст менее 57 лет. Взято 5 веток возрастом от 27 до 35 лет.
Лиственница № 2 - у Заимки Кулика, болото возраст - около 75 лет. Взято 8 веток от 16 до 29 лет.
Лиственница № 3 - на берегу Хушмы (у Пристани), почва сухая, возраст - более 57 лет. Взято 5 веток, возрастом от 29 до 75 лет.
Для каждой мутовки измерялся диаметр ветки без коры, возраст, толщина коры. Затем для диаметров 0,5 - 1,5, 1,5 - 2,5, 2,5 - 3,5 и т.д. миллиметров, т.е. со средними значениями диаметров d = 1, 2, 3 и т.д. миллиметров вычислялись средние арифметические значения толщины коры веток данного дерева 
и величины несмещенной оценки дисперсии D:
, (4)
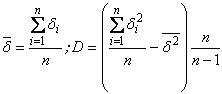
где n - количество замеров для среднего диаметра d.
Результаты вычислений сведены в табл. 1, и по этой таблице построены графики 
, приведенные на рис. 2. Из рис. 2 видно, что для диаметров d от 0 до 10 мм зависимость , можно аппроксимировать линейной функцией
δ = ad + δ0, (5)
где величина a = const для данного дерева, а δ0, приблизительно одинаковая для всех деревьев, равна 0,4 мм.
Подставляя (5) в (1), получаем:
(6)
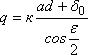
отсюда:
(7)
Для лиственницы № 2 величина с2 ~ 3 мм для № 1 и № 3 с2 ~ 7 мм.
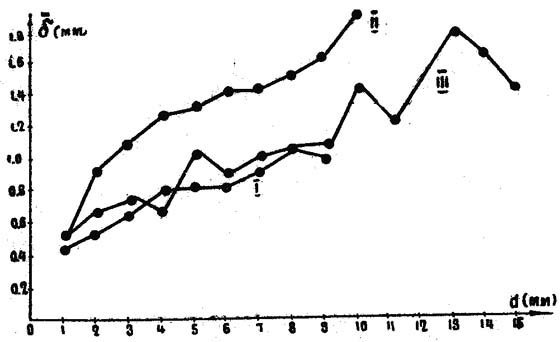
Рис. 2. Зависимость средней толщины коры от диаметра ветки для трех лиственниц.
Рассматривая равенство (7), видим, что существует минимальный порог энергии q = qmin, при котором поражения камбия ветки не происходит, т.е. e = 0 при d = 0.
qmin = кδ0. (8)
Зависимости между e и d соответствующие формуле (7), построенные для ряда значений q, сравнивались с экстремальными зависимостями e (d), построенными для некоторых поражений веток лиственниц. Следует заметить, что при малых диаметрах они сильно отличаются от теоретических. Действительно, как правило, кончики веток, имеющих поражения 1908 года, сухие, т.е. имеют e = 360°. Затем с увеличением диаметра идет обычно резкий спад кривой до e < 180° и далее, e изменяется почти по косинусоиде. Это связано, главным образом, с тем, что все наши рассуждения, приводятся без учета теплопроводности коры и древесины, которая, очевидно, будет способствовать расширению угла e и тем значительнее, чем меньше диаметр ветки. Действительно (рис.1), участки коры и камбия, расположенные под углом к плоскости падения фронта светового излучения, разогреваются не только за счет поглощения световой энергии, но и за счет притока тепла от соседних, более нагретых участков коры и древесины. Это выразится в увеличении угла e по сравнению с расчетным. Однако при увеличении диаметра ветки теплопроводность играет все меньшую роль, что показывает довольно хорошее совпадение расчетных и экспериментальных зависимостей при больших диаметрах. Заметим, что провал на одной из кривых рис. 36 можно объяснить экранировкой этого участка ветки соседней веткой или боковым отростком этой же ветки, или местным утолщением коры.
Таблица толщины коры веток
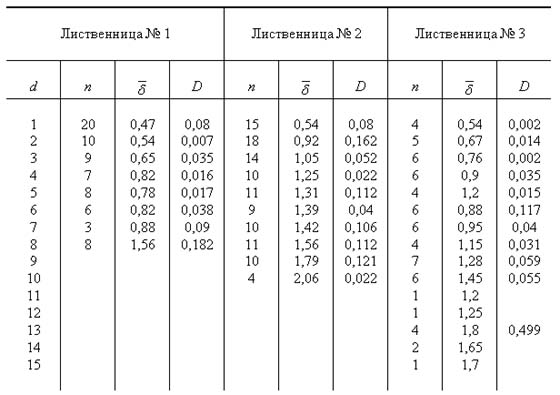
n – число замеров для среднего диаметра, - средняя толщина коры, D – несмещенная оценка дисперсии
Иногда, чаще к границе ожога, встречаются ветки, концы которых остались, живыми, и поражение начинается на некотором расстоянии от конца ветки. ε таких поражений с увеличением диаметра ветви сначала увеличивается до ε 180˚, затем идет обычный спад до ε=0. Это может быть объяснено значительной экранировкой концов веток живой хвоей, которая здесь особенно развита. Для проверки этого предположения были подсчитаны количества пучков живой хвои на разных по толщине участках ветвей, взятых с тех же, указанных ранее, трех лиственниц. Оказалось, что затененность ветки с увеличением диаметра падает (рис. 5). Кроме того, это можно объяснить резким изгибанием конца ветки кверху, что способствует уменьшению угла падения вектора светового потока. Из (6) видно, что величина q для каждой ветки пропорциональна максимальному пораженному диаметру. Действительно, при ε = 0 ,
q = к(ad0 + δ0)
то eсть по величине максимального пораженного диаметра можно судить о величине световой энергии, падающей на данную ветку.
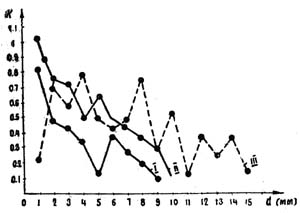Рис. 5. Зависимость среднего количества пучков живой хвои на единицу длины ветки (К) от диаметра ветки для трех лиственниц.
Необходимо получить точные данные по теплофизическим свойствам коры, что позволит перейти от качественных к количественным оценкам плотности светового потока в каждой точке. Необходимо оценить ошибки данного метода. Решение задачи с учетом теплопроводности позволит более детально вникнуть в механизм явления.