Нестационарные явления при быстром торможении тел в гиперзвуковом потоке
Н.В.Попеленская
Институт механики МГУ им. М.В. Ломоносова, Москва
Оценка характерного времени торможения тела
Проведем оценку характерного времени торможения для крупного метеорного тела сферической формы, движущегося в гиперзвуковом потоке. Запишем уравнение движения тела в атмосфере в пренебрежении боковой силой и весом:
(1)
Здесь и далее M - масса, V- скорость тела, S- площадь миделева сечения, t - время, 
a - плотность атмосферы, b- плотность тела, Cd - коэффициент аэродинамического сопротивления. Определим характерное время торможения формулой 
. Тогда из (1) получим 
. Используем коэффициент формы тела 
, где W - объем тела. Тогда
и 
. Последнюю формулу можно видоизменить, если заметить, что величина 
есть характерное время обтекания тела. Для сферы величина
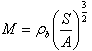
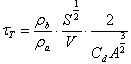
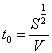
~ 1 (2)
Тогда получим, что 
T/t0 ~ b/a или
T ~ t0 при b ~ a (3)
Таким образом, нестационарное обтекание при торможении достигается для плотностей тела, сравнимых с плотностью атмосферы в окрестности тела.
Оценка характерного времени абляции тела
Уравнение для переменной массы тела в предположении, что весь тепловой поток от окружающего газа идет на испарение материала поверхности, имеет вид
(4)
где H* - теплота сублимации, Ch - коэффициент теплообмена. Определим характерное время абляции как 
. Тогда из (4) следует:
.
Используя параметр уноса массы 
[1], получим:
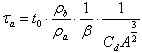
Таким образом, принимая во внимание (2), получаем
a ~ t0 при b ~ 
a . (5)
То есть нестационарное обтекание при абляции достигается для отношений плотности тела к плотности атмосферы в окрестности тела, сравнимых с параметром уноса массы, который может быть очень большим.
Предположение о возможной эволюции тела в гиперзвуковом потоке
Так как по мере продвижения вглубь атмосферы плотность увеличивается, то из полученных оценок следует, что при >1 условие (5) наступает на большей высоте, чем условие (4) при одинаковом b. А значит, заметное испарение начнется раньше, чем заметное торможение. Таким образом, на некотором этапе эволюции тело может полностью перейти в газообразное состояние, частично сохраняя сплошность и до окончания торможения. Возможно, что именно это произошло при падении Тунгусского метеорита. В пользу этой гипотезы есть два подтверждения. Во-первых, то, что за 95 лет поисков не был найден ни один фрагмент метеорита. Во-вторых, то, что столь огромное разрушительное воздействие не могло быть вызвано отошедшей ударной волной. Вероятно, газовое облако дошло до поверхности Земли, и его распространение по ней вызвало вывал леса и другие последствия.
Литература
- Стулов В.П., Мирский В.Н., Вислый А.И. Аэродинамика болидов. Наука. Физматлит, 1995, 240с.