Д. Ф. Анфиногенов, Л. И. Будаева
ТОО ТРОЦ, ТГУ, Томск
Показания очевидцев Тунгусского феномена, собранные в том же 1908 году, дают достаточные основания для ряда исходных определенных выводов о характере этого явления. Несмотря на стремительность развития событий, наблюдатели отметили последовательность изменений формы светящейся части ГТБ: «шар» —«бревно» — «комок огня в лобовой части» — «вспышка на уровне горизонта» [4].
Последовательность изменения огневых форм указывает на то, что имели место характерные явления для болида, образованного компактным твердым телом, при последовательном погружении метеороида в атмосферу на гиперзвуковой скорости с возрастанием энерговыделения по мере нарастания ее плотности и, следовательно, удельного сопротивления вторжению ТКТ, с масс-энергетической разрядкой — форсированной потерей массы и энергии (зона так называемой «задержки», или максимального торможения тела или его фрагментов) в приповерхностных слоях атмосферы.
Яркость излучения болида приравнивалась наблюдателями к солнечной, даже при одновременном нахождении ТФ и Солнца в поле зрения наблюдателей со среднего течения Ангары.
При этом среднее расстояние до ТФ при самых умеренных посылках составляло около 300 км. Учитывая, что световой поток солнечной энергии на расстоянии Земли составляет 1373 Вт/м2 (в среднем) [11] или 1,4 1010эрг/м2с, а также то, что потери солнечной энергии в атмосфере в тот день были незначительными, поскольку погода определялась как «ясная» и «чрезвычайно ясная», можно оценить излучательную мощность (W) болида по формуле:
![]()
где R — радиус сферы, равный среднему расстоянию от ГТБ как источника излучения до наблюдателей ( 3*105 м).
Отсюда — верхняя оценка мощности ГТБ в стадии «полета»:
![]()
Принимая долю световой энергии в 30 % от общего энерговыделения, можно оценить полную мощность ГТБ в стадии «полета» средней величиной
![]()
Учитывая, что в конечном счете энерговыделение обусловлено полным торможением части массы, потерянной ТКТ при взаимодействии с атмосферой, а, следовательно, и части кинетической энергии, можно определить диапазон средних величин вещественных потерь ТКТ на довзрывной стадии полета, в единицу времени, приняв, в качестве оценочного, диапазон атмосферных гиперзвуковых скоростей от 20 км/с до 40 км/с
![]()
при и vТКТ = 20 км/с
![]()
при vТКТ = 40 км/с
Сделанные оценки есть достаточное основание считать Тунгусский феномен 1908 года классическим, но гигантским по обыденным меркам болидом (ГТБ), образованным компактным ТКТ, вероятно, перешедшим на «полпути» в компактный рой его фрагментов.
Подчеркнем: сделанные оценки по масс-энерговыделению на стадии «полета» мы считаем реалистическими, но верхними из реалистических. Однако, порядок величин определяется достаточно верно и этот порядок свидетельствует, что еще до «взрыва», на стадии «полета», мощность ГТБ соответствовала по эквиваленту предмегатонному диапазону, и ничего не может быть удивительного в том, что в самых нижних и самых плотных слоях атмосферы, так сказать, на финише, выделилась энергия мегатонного диапазона.
В 1965 году нами было предложено решение обратной задачи построения начальной формы ударной волны (на участке сильной ударной волны) по совокупности характеристик вывального разрушения леса. Осуществлена интерпретация природы источника ударной волны, что нашло свое отражение в докладе на метеоритной конференции (Новосибирск, 1965) [1] и в развернутом докладе на XIII Всесоюзной метеоритной конференции (Москва, 1968).
Учитывая эмпирические закономерности, установленные в модельных экспериментах, можно утверждать, что угол наклона осесимметричного источника, определяемый по внешним границам вывала леса, имеет завышение по отношению к углу, определяемому по геометрии внутренних границ сплошного вывала леса и местоположению псевдоэпицентра относительно них, на 15—20°. Введение этой поправки показывает, что в действительности наклон оси составлял от 25° до 30°.
Ударная волна в головной части ГТБ по ходу движения ТКТ и продуктов его распада не имела усиления и не имела сплошного выпуклого фронта, но в целом она была осесимметричной и действовала в стороны от оси уже на расстоянии в несколько километров как почти идеальная в геометрическом смысле волна, со сплошным фронтом и энергетической подпиткой с верхних участков, имеющих протяженность в атмосфере не менее, чем вдвое большую протяженности источника непосредственно над территорией вывала деревьев (так называемая полубесконечная осесимметричная волна с неравномерным распределением энергии вдоль ее оси по принципу «веретена» — поуже и пожиже кверху и книзу в первом приближении).
Суммарная энергия, выделившаяся на действующем участке «полубесконечного» источника определена нами методом сравнения с энергией термоядерного воздушного взрыва по разрушениям на местности, при этом использованы критерии и номограмма, представленные в сборнике данных по действию ядерного оружия [5].
Радиусы сильного и среднего поражения нами определены соответственно по площади сплошного повала деревьев на Куликовском вывале леса (площадь —до 600 км2) и из площади среднего повала деревьев, принятая как средняя площадь между величиной площади сильного и слабого вывала леса (1/2 суммы 600 км2 + 2150 км2 = 1385 км2), по формуле
![]()
где Rэфф — эффективный радиус действия сферической волны эквивалентной мощности; S — площадь вывала. Расчеты показали, что
Rсильное 13,8 км,
Rсреднее 21,0 км,
что по приведенной в сборнике номограмме дает очень близкие значения энергии по обоим радиусам —
8 Мт или 3,36 1023 эрг.
В данном случае это суммарная оценка всей выделившейся энергии на действующем участке траектории от высот 45—50 км до высоты 3—5 км.
Следует повторить, что полученные по величинам периодов инфразвуковых волн данные об энергетике явления могут быть завышенными из-за растягивания исходной волны осесимметричным источником энергии, имеющим протяженность, сравнимую с длиной формирующихся инфразвуковых волн.
Строго говоря, для самых распространенных скоростей движения метеороидов в земной атмосфере физической теории не существует, поскольку не проведены управляемые эксперименты по метанию тел в атмосферу Земли.
Пассивно-наблюдательные эксперименты не охватывают всех вариантов и диапазонов даже внешних характеристик тела и его движения в атмосфере. Уже накопленные данные инструментальных наблюдений (данные болидных сетей, метеорных патрулей) подчеркивают богатство вариантов и даже на начальных этапах формирования болидов — когда имеют место слабые относительные колебания величин по основным параметрам движения — изменения скорости, массы и формы тела, параметров окружающей, особенно по курсу, атмосферы, что уж говорить о заключительных этапах.
Выше мы определили, что полная энергия осесимметричного источника над районом катастрофы составляла
8 Мт или 3,36 1023 эрг.
При определенных нами углах наклона оси источника в 25—30° к поверхности земли в земной точке можно произвести оценку массы воздуха, которая потребуется для того, чтобы преобразовать кинетическую энергию ТКТ или его фрагментов в ударную волну при наиболее устоявшихся оценках атмосферной скорости ТКТ и средней плотности вещества метеоритов.
Цель данного расчета только одна — оценить и, по возможности, сузить физические рамки, в которые укладывается ГТБ, и выйти на судьбу вещества ТКТ.
Для начала возьмем среднее геометрическое крайних значений атмосферных скоростей метеороидов
![]() км/с.
км/с.
У этого значения скорости не меньшие основания быть избранным для примера, чем у соседних. Угол наклона оси источника определим в 28° — угловая высота радианта Солнца на момент События. Принимая приведенную высоту однородной атмосферы равной 8 км, введем поправку, исключающую нижний слой атмосферы от уровня моря до нижней точки источника, определяемой по конфигурации внутренней границы сплошного вывала со значением около 5 км. Это составляет 3,8 км и ее остаток сверху — 4,2 км.
![]()
где Mвозд— требуемая масса воздуха, vTK— входная атмосферная скорость ТКТ, приравненная нами к 28,4 км/с.
Находим
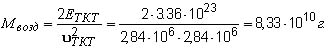
Объем воздуха при ![]() кг/м3 составит
кг/м3 составит
![]()
Определим поперечное сечение наклонного столба воздуха по формуле

где 4,2 103 м — остаток сверху приведенной к однородной атмосферы, 28° — угол наклона оси источника.
![]()
Диаметр наклонного воздушного столба находится по известной формуле

Поскольку масса ТКТ также равна массе воздушного столба — равноправного участника События, — то, задавая плотность вещества ТКТ и форму тела, оценим габариты ТКТ.
Возьмем два значения плотности ТКТ: 8 103 кг/м3 и 3,5 103 кг/м3, примерно соответствующих плотностям вещества железного и каменного метеоритов, и зададим ТКТ форму шара, тогда
![]()
где MTKT =Mвозд.ст..
Получим 1) для железного метеорита
![]()
откуда находим радиус ТКТ
![]()
и площадь поперечного сечения ТКТ
![]()
При этом
![]()
Поставим задачу «закрыть» поперечную площадь воздушного столба округлыми обломками ТКТ (в нулевом приближении — шарами по форме).
Из известного закона соотношения поверхностей или площадей сечения материнского шара и производных от него, который гласит, что суммарная площадь сечений обломков обратно пропорциональна радиусам. Отсюда
![]()
объем среднего обломка-шара
![]()
и таких обломков будет
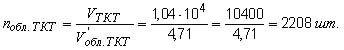
2) Объем каменного ТКТ и все остальные характеристики находятся аналогичным образом
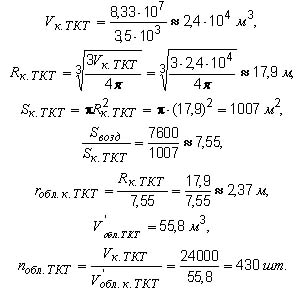
Усредненная масса одного обломка — будет соответственно равна:
1) для железного метеорита » 38 тонн;
2) для каменного метеорита » 195 тонн.
Встает вопрос: могут ли такие «дробины» исчерпать себя в атмосфере полностью? Поскольку теория болидных образований для крупных и массивных тел находится до сих пор в стадии разработки и идут споры о том, какими формулами, уравнениями и коэффициентами и их значениями пользоваться в том или ином случае, обратимся к наблюдательной эмпирии.
По совокупности характеристик, среди которых разграничивающей была потеря массы тела за единицу времени, в качестве массивных крупных метеороидов, чьи болиды были пойманы Прерийной и Европейской болидными сетями [7; 12], были отобраны имеющие расчетную массу 1000 кг и более.
И поскольку из-за большого числа характеристик, влияющих на болидообразование (из-за большого разброса их значений и малого числа наблюдений) не выявлялось строгой закономерности, выстраивающей их в причинный ряд (ряды), мы их объединили в группы по месту регистрации и без большей дифференцировки.
Для каждой группы составили образ синтетического болида с усредненными значениями по группе для каждой из имеющихся характеристик.
Полученные образы болидов на удивление близки.
Еще раз подчеркиваем определенную искусственность этих построений, но, по крайне мере, для обеих групп вместе имеются болиды, расположенные, по главным энергетическим характеристикам, по «обеим» сторонам относительно найденных средних величин и положений.
Что следует из этих сведений?
Для нас — главное: на скоростях более 20 км/c (средняя для обеих групп — 22,8 км/c; здесь следует напомнить о критической скорости в 22 км/c, определенную в работе [10] как гипотетический рубеж «непробивания» атмосферы метеороидом и его фрагментами) на высотах 45—35 км может происходить «сжигание» метеороидов (крупных!) со скоростью 15 т/с и выделением энергии болида средней мощности 3,9 1019эрг/с.
По калибру — это мелкокалиберная «атомная» бомба примерно в 1 килотонну.
Геометрия вывала леса в зоне масс-энергетической разрядки ГТБ, показывает, что верхняя часть этой зоны при = 28° расположена на высоте около 15 км. Отношение плотности атмосферы на этой высоте к плотности атмосферы на высоте верхней точки масс-энергетической разрядки «синтезированного» из наблюденных болидов составляет
![]()
Отсюда: даже при скорости усредненно-синтезированного из наблюденных болида на этой высоте реально сжигание метеороида со скоростью
![]()
Или сжиганию фрагментов крупного метеороида такой же массы в секунду. А поскольку скорость сжигания массы метеороида зависит еще и от куба скорости, то взяв соотношение куба скорости, принятой в примере для ТКТ (28 км/с) к кубу скорости синтез-болида, получим более высокое значение мощности «сжигания»
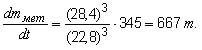
А ведь атмосферная скорость ТКТ могла быть и выше при вполне вероятных вариантах его доатмосферной и атмосферной траекторий.
Например. Средняя скорость метеороидов из состава того же метеорного дневного потока -Таурид, пик активности которого приходится почти на день События составляет 31 км/с.
И мощность сжигания метеороидов поднимется до 861 тонны в секунду или, что, наверное, точнее и правильнее, сжигания отдельного метеороида массой в 861 тонн или эквивалентного ему «куска» на лобовой поверхности метеороида, значительно превосходящего габаритами метеороид с данной массой.
Рассмотрим силовые нагрузки на твердое тело крупного метеороида, при которых проявляются различные прочностные качества последнего и тем или иным способом определяют и судьбу метеороида и тип болида…
Величины удельного сопротивления метеороида выводятся из формулы метеорно-болидной физики [2], связывающей лобовое сопротивление метеороида с площадью его поперечного сечения (миделем), скоростью полета на определенной высоте и плотностью воздуха на этой высоте через безразмерный коэффициент Г
![]() (1)
(1)
и удельное сопротивление будет равно
![]() (2)
(2)
Принимая для крупных тел и скоростей, больших второй космической для Земли, [3] и приравнивая значение постоянной тяготения на поверхности Земли к 10 м/с2, получаем простую формулу (3)
![]()
С помощью этой формулы, используя пороговые прочностные характеристики тех или иных тел и веществ, можно определить их участь на различных высотах и скоростях полета.
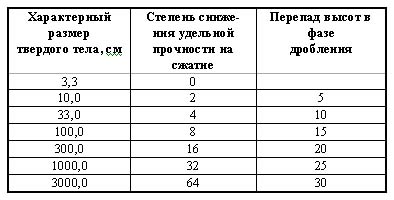
Прежде чем рассмотреть несколько характерных примеров использования этой формулы по профилю наших интересов совершим короткий экскурс в механику твердых крупных тел. Современные исследования по этой части в горном деле и метеоритике [9; 6] показывают существенную зависимость между удельной прочностью тела, его объемной формой и размерами по линии нагрузки, при этом для естественных тел (блоков горных пород и их массивов) и для искусственных тел, выработавших свой ресурс, зависимость от линейных размеров является сильной. Даже на уровне лабораторных образцов, вырезанных из естественных блоков породы, предел прочности кубика с ребром в 3 см в два раза выше удельной прочности кубика с ребром в 10 см [9]. Подобная зависимость имеет место и на более крупных образцах, в том числе — из метеоритного вещества, в частности, из экземпляров замечательного каменного дождя Царев [6].
Если экстраполировать зависимость, характерную для дециметрового диапазона размера твердых тел на метровый диапазон и первые десятки метров (это касается естественных твердых тел многомиллионнолетнего возраста), то различие между удельной прочностью на сжатие габаритных тел может в несколько десятков раз отличаться от предела прочности вещества на сжатие, характерного для бездефектной бестрещиноватой вырезки малых размеров из материнского твердого тела. На практике это наблюдается сплошь и рядом в виде поэтапного на разных высотах дробления метеороидов, заканчивающегося иногда (и не так уж редко) потрясающими метеоритными дождями и эллипсами рассеивания выпадений или так называемыми «медузами» — следами разорвавшегося на мелкие куски метеороида, «разлетающиеся» от места разрыва и сгорающие в атмосфере в виде извивающихся микроболидов — «щупалец».
Оценим согласно формуле удельного лобового сопротивления (3) перепад высот, на котором тела разных габаритов будут дробиться. Отметим при этом, что процесс дробления любого конкретного метеороида — сугубо индивидуальный процесс, определяемый, как было сказано выше, целым набором характеристик. Из формулы следует, что при одной и той же скорости росту удельного сопротивления в 2 раза соответствует перепад высот примерно в 5 км (по перепаду плотности в изотермической атмосфере).
В реальности параллельно процессу дробления идет разрушение метеороида путем испарения при лучистом нагреве его поверхности, при прямом воздействии потоков обтекания и т. п. На скоростях заметно выше второй космической процесс испарения становится определяющим и возможна ситуация, когда процесс дробления по ступеням будет «срываться» процессом прогрессивного испарения. В реальности эти процессы взаимодополняют друг друга, усиленно дезинтегрируя метеороид (особенно крупный). И чем крупнее метеороид, тем интенсивнее. Но до определенных размеров, естественно. И верхний предел еще не установлен.
Начнем с базового варианта.
В верхней точке дробления . Это значение близко к скорости входа ТКТ в атмосферу. Интервал высот что для железного ТКТ, что для каменного, согласно таблице, — около 30 км. К точке активного торможения и «сжигания»-испарения (то есть к зоне масс-энергетической разрядки) на высоте около 15 км ТКТ подходит в виде компактного роя фрагментов, площадь суммарного поперечного сечения которых соответствует поперечному сечению наклонного столба воздуха, необходимого и достаточного, чтобы «извлечь» из фрагментов ТКТ почти всю кинетическую энергию. Из этого ограничения следует, что начало дробления ТКТ было положено на высоте около 45 км.
Вряд ли это дробление было одномоментным и на равные обломки, но разброс размеров обломков не должен был быть значительным, иначе изменилась бы структура болида в головной части. Будучи достаточно крупными — несколько десятков — несколько сот тонн, — обломки летели плотным роем, но распределенными по направлению полета как на эллипсах рассеяния метеоритов, в идеале их рой можно так и представлять себе как горизонтальный, расширяющийся, но незначительно, эллипс рассеяния малых размеров, таких, чтобы болиды каждого отдельного фрагмента оставались в энергетическом пространстве других обломков и роя в целом. До высоты около 5 км обломки тормозятся и испаряются до скорости в 22 км/с и 1/3 массы каждого, не достигая предела прочности их вещества на сжатие.
Возьмем предельный случай в конце траектории на высоте 5 км.
![]()
прочность вещества ТКТ и его обломков должна быть не ниже
![]()
Такой предел прочности на сжатие имеют некоторые высокопрочные каменные метеориты (тот же метеорит Царев), каменное литье из базальта, железные и, вероятно, железо-каменные метеориты.
При этом вещество ТКТ должно иметь повышенную испаряемость. Сочетание этих характеристик возможно, например, при наличии в структуре вещества ТКТ полупрозрачных зерен (в том числе для ультрафиолетовой части спектра, например, кварца) [8], возможны и другие варианты.
Сколько бы вариантов мы не обсчитывали еще, базовый вариант останется базовым для осознания судьбы вещества ТКТ. Основная масса ТКТ в виде роя его фрагментов «сгорела» в холодно-плазменном реакторе ГТБ на нижнем участке траектории, превратившись в ультрадисперсную и высокодисперсную порошкообразную аэрозоль, частично агрегированную путем спекания в более крупные частицы субмикронного и микронного размеров.
На наш взгляд, основным направлением в поисках вещественных следов ТКТ, до 100-летия проблемы, должен стать поиск жаропрочных химически инертных вещественных микроагрегатов, продуцированных в холодно-плазменном реакторе ГТБ, и зафиксированных в стратифицированных природных объектах и коллекторах.
Ударные (кинетические) температуры в осевой части болидов крупных метеорных тел достигают нескольких сот тысяч градусов, в зависимости от скорости метеороида [3], приводящих к образованию неравновесной так называемой холодной плазмы с эффективными температурами ионного газа-плазмы в несколько десятков тысяч градусов и температурой электронного газа, сравнимой с ударно-кинетической температурой на лобовой поверхности метеороида, точнее — между нею и фронтом ударной волны, образуемой в таких случаях. Через лучистый нагрев зона действия плазменного реактора распространяется (в зависимости от мощности болида) на расстояние от нескольких сот метров до первых километров от оси болида. Испарившееся вещество метеороида, пройдя через холодно-плазменный генератор образованного метеороидом болида и взаимодействуя с составляющими воздуха, в первую очередь — с азотом, превращаются в ультрадисперсную и высокодисперсную аэрозоль, которая в зависимости от состава вещества метеороида, состава атмосферы и энергетики болида может агрегироваться в более крупные частицы — слипаться, сплавляться. Обычной в таких случаях должна быть высокодисперсная порошкообразная аэрозоль.
При скоростях, близких ко второй космической (начальной и остаточных), метеороид и его болид генерируют дымы и туманы, в последних образуется шариковидная микрокапельная аэрозоль, доля которой в продукции холодно-плазменного реактора болида составляет проценты и доли процента.
Судя по суммарной энергии, выделившейся в зоне масс-энергетической разрядки ГТБ (до 8 Мгт), ХПР ГТБ будет сформирован в течение менее одной секунды (время полета обломков ГТБ в зоне). Его объем составит, по аналогии с термоядерным взрывом такой же мощности, около 27 км3.
Неравновесность плазмы характеризуется высокими температурными градиентами, как по оси ГТБ, так и от оси к периферии, достигающими десятков тысяч градусов в секунду и на километр габаритов ХПР, со временем жизни ХПР в несколько десятков секунд. При этом активность и долгожительство ХПР поддерживалось энергией и температурой электронного газа. В этих условиях ХПР сработает как плазменный генератор начала века по производству из воздуха окислов азота и в конечном счете — азотной кислоты. Только мощность технического ХПР столетней давности не идет ни в какое сравнение с мощностью ХПР ГТБ. На качественном уровне, по условиям термодинамики, азот воздуха в первую очередь свяжет кислород, причем не только из воздуха, но и кислород испарившегося и диссоциированного вещества обломков ГТБ.
Часть кислорода будет связана атомами металлов из состава метеороидов, в первую очередь — кремния, алюминия, магния, хрома, если это будет обычный каменный или железокаменный метеорит. Поскольку дефицит кислорода в таком случае будет очевиден, начнется образование более экзотических соединений: нитридов, в первую очередь нитрида кремния, силицидов и других подобных соединений.
В случае углистого хондрита будут образовываться карбиды и даже возможно образование аморфного алмаза.
В результате преобладающих реакций в ХПР происходит образование до 2—3 млн. тонн окиси азота, до 2,5—3,5 млн. тонн молекулярных соединений азота (N2, N3, N6), более 100 тыс. тонн трудноразлагаемых нитридов и силицидов металлов из состава ТКТ (Si3N4, TiN, AlN, Fe3Si2, TiSi2, CrSi2, ZrSi2 и др.), которые являются экзотическими маркерами катастрофы 1908 года. За пределами ХПР окись азота окисляется до двуокиси, а при взаимодействии их с парами воды, водой и земной пылью образуются кислоты (азотистая, азотная, азотистоводородная) и продукты их воздействия на земные среды и объекты.
Имеются достаточные основания допустить, что 1) загадочный равномерный ожог растительности и древесины; 2) «жирование» сосны и других хвойных пород (ускоренный прирост, треххвойность); 3) генетические аномалии растительности обусловлены действием агрессивных окислов азота, азотной и азотистой кислот и производными химагентами.
Изложенное является результатом качественного анализа. Считаем необходимым внести существенные коррективы в план дальнейших исследований и поисковых работ и осуществить:
— разработку количественной модели ХПР ГТБ,
— усовершенствование методики отбора проб растительных субстратов, выделения и анализа экзотических продуктов ХПР,
— изучение локального, регионального и глобального распределения продукции ХПР,
— углубленный анализ экологических последствий и имитационное моделирование воздействия вероятных продуктов ХПР на растительный и животный мир в фазе воспроизводства.
Литература
1. Анфиногенов Д. Ф. О Тунгусском метеоритном дожде // Успехи метеоритики — Новосибирск: Изд-во ИГиГ, 1966.— С. 20—22.
2. Бронштэн В. А. К вопросу о движении в атмосфере Тунгусского метеорита // Метеоритика. — М.: Наука, 1961. — Вып. XX. — С. 72—86.
3. Бронштэн В. А. Об обстоятельствах падения Каалиярвского метеорита // Метеоритика — М.: Наука, 1962. — Вып. XXII. — С. 42—46.
4. Вознесенский А. В. Падение метеорита 30 июня 1908 г. в верховьях р. Хатанги // «Мироведение». — 1925. — Т. XIV. — № 1. — С. 25—38.
5. Действие ядерного оружия. — М.: Воениздат, 1963. — 684 с.
6. Зоткин И. Т., Медведев Р. В., Горбацевич Ф. Ф. Прочностные характеристики метеорита Царев // Метеоритика. — М.: Наука, 1987. — Вып. 46. — С. 86—93.
7. Мак-Кроски Р. Е., Шао И.-И., Позен А. Болиды Прерийной сети. 1. Общие сведения и орбиты // Метеоритика. — М.: Наука, 1978. — Вып. 37. — С. 44—60.
8. Мартынюк М. М. Роль фазового взрыва космического вещества в процессе разрушения метеоритов. // Взаимодействие метеоритного вещества с Землей. — Новосибирск: Наука, 1980. — С. 168—178.
9. Прочность и деформируемость горных пород / Ю. М. Карташов, Б. В. Матвеев и др.— М.: Недра, 1978. — 269 с.
10. Симоненко А. Н. Некоторые особенности орбит метеоритов и их родительских тел // Метеоритика. — М.: Наука, 1978. Вып. 37. — С. 3—24.
11. Физические величины. Справочник. — М.: Энергоатомиздат, 1991. — С. 1232. 12. Цеплеха Зд. Болиды Европейской сети // Метеоритика — М.: Наука. — 1978. — Вып. 37. — С. 60—69.
