В.В.Светцов
Институт динамики геосфер РАН
117979, Москва, Ленинский проспект 38, корп.6
Падение гипотетического Тунгусского метеороида в атмосфере можно разделить на несколько стадий: полет целого метеороида в верхних слоях атмосферы, разрушение и дробление тела, расплющивание раздробленной массы под действием аэродинамического давления на лобовой поверхности, образование роя отдельных фрагментов и их дифференциация по размерам, образование облака пара и микрочастиц, продолжающих движение вдоль траектории. Каждая последующая стадия падения зависит от предыдущей, а сложность математического описания и моделирования отдельных стадий возрастает по мере приближения метеороида или его остатков к поверхности Земли. Для получения достаточно точных результатов при моделировании всего полета в атмосфере необходимо учитывать механику разрушения и дробления, перенос излучения, плавление, испарение, отколы, особенности сложного аэродинамического движения, конденсацию. Большое количество фрагментов разного размера делает возникающую физико-математическую задачу чрезвычайно сложной. До сих пор моделирование падения Тунгусского метеороида в атмосфере проводилось лишь при весьма упрощенных предположениях о происходящих процессах.
На первый взгляд кажется, что исследование начальной стадии полета целого тела не вызывает затруднений в рамках обычной аэродинамики. Действительно, процессы абляции не оказывают существенного влияния на полет целого крупного метеороида размером 50-100 м [1]. Вычислительные методы позволяют проводить расчеты обтекания летательных аппаратов весьма сложных конфигураций, а для тел простой формы, например, для шара хорошо известны распределения давления на лобовой поверхности и коэффициенты сопротивления. Заметим, что задача разрушения метеороида сводится обычно к вычислению напряжений внутри тела под действием квазистатических нагрузок, поскольку увеличение аэродинамических нагрузок по мере падения происходит достаточно медленно по сравнению со скоростью распространения малых возмущений в веществе метеороида.
Между тем ситуация даже на первой стадии падения гораздо сложнее, так как оказывается, что падение метеороида может сильно отличаться от полета, например, космического корабля при входе в атмосферу. Существенно более высокие скорости метеороидов (и более высокие числа Маха) вызывают частичную ионизацию воздуха за головной ударной волной, что приводит к следующим особенностям. Во-первых, значительно снижается показатель адиабаты воздуха - до 1.1 - 1.2 [2], что увеличивает сжатие газа за ударной волной и, следовательно, уменьшает расстояние между ударной волной и телом. Во-вторых, ход ударной адиабаты имеет участки с положительной производной давления от удельного объема, что может приводить к неустойчивости фронта ударной волны [3,4,5]. В-третьих, перенос излучения оказывает сильное влияние на газодинамическое течение - сжатие за фронтом головной ударной волны еще более возрастает за счет лучистого охлаждения газа и поэтому фронт самой ударной волны еще более приближается к телу. Более того, так называемое опережающее излучение, т.е. испускаемое за фронтом и поглощаемое перед фронтом ударной волны, способствует возникновению неустойчивости ударной волны [6].
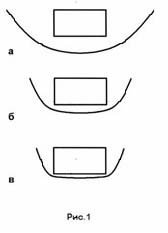На рис.1 проиллюстрированы форма и положение ударной волны по результатам расчетов обтекания торца цилиндрического тела при следующих предположениях: (а) скорость тела V=1 км/с, высота полета H=0; (б) V=15 км/с, H=40 км; (в) V=15 км/с, H=40 км, т.е. то же что и (б), но расчет проведен с учетом лучистого охлаждения газа за фронтом (диаметр цилиндрического тела был принят равным 60 м). Хорошо видно, насколько сильно ударная волна приближается к поверхности тела при повышении его скорости и интенсивности излучения.
Течение в очень тонком ударно-сжатом слое становится чувствительным к возмущениям, и поэтому возникает существенный вопрос - является ли течение устойчивым при чрезвычайно сильных сжатиях за головной ударной волной? Сжатие за фронтом пропорционально (
+1) / (-1), где g - показатель адиабаты, который может быть весьма низок для многоатомных газов [7]. Поскольку достичь высоких скоростей обтекания и больших потоков излучения в лабораторных условиях весьма сложно, то именно эксперименты с многоатомными газами могут пролить свет на проблему поведения течения в воздухе при высоких сжатиях за фронтом. Экспериментальные результаты [8] по обтеканию цилиндрических тел фреоном показали, что при числах Маха около 10 течение неустойчиво, а фронт ударной волны претерпевает чрезвычайно сильные искажения. Авторы работы объясняли возникновение неустойчивости фронта влиянием неравновесного процесса диссоциации фреона.
В настоящей работе была проведена серия двумерных газодинамических расчетов обтекания цилиндра и ступеньки совершенным газом при показателе адиабаты =1.1, что немного выше предельного значения для частично ионизованного воздуха. Расчеты проводились несколькими численными методами: Годунова [9], крупных частиц [10], TVD [11] и PPM [12] на сетках с шагом 0.01 и 0.005 от радиуса цилиндра или высоты ступеньки. При задании начальных данных в виде равномерного потока, получалось стандартное стационарное численное решение с гладким профилем головной ударной волны и непрерывным полем течения внутри ударно-сжатого слоя. Затем в набегающий поток вносилось кратковременное возмущение в виде тонкого энтропийного следа, который может быть вызван, например, частицей, вылетевшей за пределы головной ударной волны, причем длина следа составляла несколько диаметров тела. Через некоторое время тело снова оказывалось в однородном равномерном потоке газа.
Основные результаты численного моделирования (всеми методами) оказались следующими. Течение никогда не возвращается к тому стандартному стационарному решению, которое существовало до возмущения потока. Течение принимает нестационарный, колебательный характер. В результате искажения фронта головной ударной волны в ударно-сжатом слое возникают сложные возвратно-вихревые движения с внутренними ударными волнами, контактными разрывами, чередованием дозвуковых и сверхзвуковых областей. Таким образом, оказывается, что существует нестандартный нестационарный режим обтекания тел, который назван вихревым, так как именно вихревые движения в ударно-сжатом слое поддерживают искажения фронта головной ударной волны и инициируют процесс возникновения этого режима.
На рис.2 показана форма головной ударной волны для двух моментов времени при обтекании бруска с бесконечной шириной в направлении перпендикулярном плоскости чертежа. Набегающий поток направлен слева направо, число Маха равно 60, =1.1. Затенены области дозвукового течения. Расчет проведен методом PPM на сетке с шагом 0.01. Аналогичные результаты с вихревым режимом течения, полученные методом Годунова на сетке с шагом 0.005 для =1.05, проиллюстрированы на рис.3.
Вариация показателя адиабаты газа привела к следующим результатам численного моделирования. При увеличении g вихревой режим в конце концов исчезает, то есть решение во всех случаях через некоторое время приходит к стандартному виду. Предельные значения g зависят от метода вычислений, его точности и вносимой им численной вязкости. Метод Годунова на сетке с шагом h=0.005 дает вихревые режимы до =1.14 при обтекании ступеньки и до =1.24 при обтекании цилиндра. Метод PPM, обладающий гораздо меньшей вязкостью, дает предельные значения =1.17 и =1.35 при обтекании ступеньки и цилиндра, соответственно. Уменьшение показателя адиабаты до 1.03 приводит к тому, что все указанные методы, кроме наиболее вязкого метода крупных частиц, дают лишь вихревой режим обтекания. Другими словами, если даже в поток не вносятся возмущения, численное решение от стандартного режима течения спонтанно переходит к вихревому. В некоторой промежуточной области показателей адиабаты газа в зависимости о начальных данных могут реализоваться оба режима обтекания тела - стандартный и вихревой. Отметим, что, хотя =1.03 существенно ниже предельной величины =1.1 для воздуха, рассмотрение столь низких значений имеет смысл, так как по влиянию на сжатие газа и отход ударной волны искусственное уменьшение эквивалентно действию лучистого охлаждения.
Аспект проблемы обтекания тела, затронутый в данной работе, ранее почти не исследовался. Полученные результаты по вихревому режиму обтекания являются абсолютно новыми и для их уточнения потребуются дальнейшие исследования. Но уже первые результаты расчетов позволяют сделать некоторые конкретные выводы, касающиеся метеорных тел. Особенности вихревого режима обтекания таковы, что свечение и абляция метеороида в этом режиме будут происходить более интенсивно благодаря большим скоростям вихревого движения, большим скоростям газа вдоль лобовой поверхности метеороида и, следовательно, интенсивному перемешиванию воздуха с парами тела и нагреву пара, вовлеченному в вихрь, до высоких температур. Весьма важно, что в вихревом режиме давление в отдельных точках поверхности тела значительно выше, чем давление торможения rV2, так как за искаженными участками головной ударной волны с большим наклоном к поверхности тела образуются высокоскоростные плотные струи, тормозящиеся на лобовой поверхности.
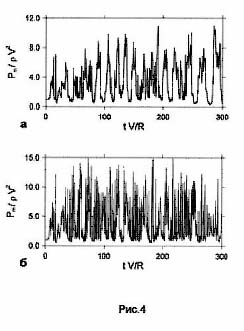Временные зависимости максимального давления на лобовой поверхности ступеньки высотой R, обтекаемой совершенным газом с g=1.1 в вихревом режиме, приведены на рис.4. Расчеты выполнены методом PPM на сетках с шагом 0.01 (а) и 0.005 (б). Пики давления на порядок выше rV2. Характерное время осцилляций давления примерно равно 10R/V. Поскольку скорость звука в теле обычно на порядок меньше скорости входа метеороида в атмосферу, то и время распространения звуковых возмущений внутри тела оказывается того же порядка, что и время осцилляций давления на лобовой поверхности. Поэтому аэродинамические нагрузки на тело не могут считаться квазистатическими. Очевидно, что более высокие (по сравнению со стандартным случаем) давления, периодически действующие в отдельных точках поверхности тела, гораздо более эффективны для разрушения метеороида.
Приближенные модели для полета Тунгусского метеороида в атмосфере [13,14,15] используют оценочные значения как для скорости поперечного растекания раздробленной массы под действием аэродинамических нагрузок, так и для коэффициента абляции. Изменение коэффициента сопротивления в два раза (сфера - цилиндр) и применение разных оценок скорости испарения поверхности тела (коэффициента абляции) сдвигает результаты, получаемые по этим моделям, таким образом, что при разных значениях коэффициентов оказывается, что с данными натурных исследований лучше согласуется то каменный астероид, то углистый хондрит, то ледяное тело [16]. Зачастую это вызывает споры, сводящиеся к тому, чья оценка лучше (неразрешимые без соответствующих экспериментов и тщательного, и очень трудоемкого, численного моделирования).
Существование вихревых режимов обтекания ставит по-иному вопрос о моделировании полета гипотетического Тунгусского метеороида. Пусть по каким-либо причинам в верхних слоях атмосферы устанавливается вихревой режим обтекания метеороида. Тогда высота разрушения тела возрастает по сравнению со стандартным режимом на десятки километров, скорости поперечного растекания раздробленной массы и абляции также возрастут по крайней мере в несколько раз. Лишь каменное тело способно при этом достигнуть высот 5-10 км, не выделив основную долю своей кинетической энергии значительно выше. Таким образом, вопрос сводится к тому, в каком режиме обтекания происходило падение Тунгусского метеороида.
Показатель адиабаты воздуха за фронтом ударной волны оказывается меньше 1.15 в широком диапазоне скоростей, характерных для метеороидов. Эффектами неравновесной ионизации за фронтом головной ударной волны можно пренебречь, так как размер зоны релаксации за фронтом весьма мал, а Тунгусское тело имело весьма значительные размеры. Лучистое охлаждение ударно-сжатого газа при скоростях 20 км/с и выше, характерных для тел кометного происхождения, может повысить сжатие на два порядка. Таким образом, необходимое условие осуществления вихревого режима - чрезвычайно большие сжатия газа - выполнено при падении Тунгусского метеороида.
Развитие вихревого режима могут инициировать различные факторы. Например, пылевые частицы, опережающие метеороид при входе в атмосферу хотя бы на несколько долей его размера, или мелкие осколки метеороида, способные выскочить за пределы чрезвычайно тонкого ударно-сжатого слоя. Движение вдоль поверхности тела первоначально холодного и плотного пара может вызвать на границе пар - воздух неустойчивость Кельвина-Гельмгольца, которая в силу тонкости ударно-сжатого слоя захватит и сам фронт ударной волны. Вопрос о гидродинамической устойчивости самого ударного фронта остается открытым, так как ход ударной адиабаты нарушается сильным влиянием излучения. Представляется, что для метеороида плохо обтекаемой формы (параллелепипед, цилиндр) наиболее вероятно осуществление полета именно в вихревом режиме со всеми вытекающими последствиями. Возможно, что регмаглипты на поверхности метеоритов - следы такого вихревого режима обтекания. Ледяное или рыхлое тело плохо обтекаемой формы выделило бы свою энергию в атмосфере намного выше предельной оценки высоты Тунгусского взрыва в 10 км.
Вряд ли вихревой режим обтекания может осуществляться для тел хорошо обтекаемой формы (конус, вытянутый эллипсоид) так как вихревые образования будут уноситься вниз по течению потоком, имеющим значительную среднюю скорость вдоль наклонной (к скорости потока) образующей тела. Поэтому заостренные тела хорошо обтекаемой формы, вероятно, обтекаются стандартным образом даже при высоких скоростях и сжатиях за фронтом. Таким образом, хорошо обтекаемое каменное тело, соответствующее Тунгусскому явлению, проникло бы глубоко в атмосферу, на высоты, которые слишком малы для объяснения, например, характера вывала леса. Итак, мы приходим к следующему выводу. Тунгусскую катастрофу могло вызвать как ледяное тело хорошо обтекаемой формы (при полете в стандартном режиме), так и каменный метеороид с большим коэффициентом сопротивления (с образованием вихревого режима обтекания). Вряд ли в ближайшее время можно будет отдать предпочтение одной из этих версий лишь на основании результатов математического моделирования падения гипотетического Тунгусского метеороида в атмосфере.
К сожалению, нет данных о составе и форме малых тел кометной природы, более того, никто никогда не наблюдал комет размером существенно менее километра. Между тем, состав мелких кометных тел может отличаться от состава известных крупных комет, так как большая доля легко испаряемых соединений в этих малых телах может улетучиться под действием солнечного излучения в космосе. Судить о составе Тунгусского метеороида по найденным элементным и изотопным аномалиям в слоях торфа и составу микрочастиц, обнаруженных в смоле хвойных деревьев, переживших катастрофу, также следует с осторожностью, так как весьма вероятно, что это лишь конденсат вещества Тунгусского космического тела. Состав же сконденсировавшихся частиц может существенно отличаться от первоначально испаряемого вещества и зависит от условий конденсации, то есть от параметров течения на поздней стадии полета облака пара и микрочастиц Тунгусского тела. Поэтому необходимо продолжать теоретические исследования и численное моделирование падения Тунгусского метеороида в атмосфере.
Литература
1. Svetsov V.V., Nemtchinov I.V., Teterev A.V., Disintegration of large meteoroids in Earth’s atmosphere: Theoretical models. Icarus. 116, 131-153, 1995.
2. Кузнецов Н.М. Термодинамические функции и ударные адиабаты воздуха при высоких температурах. М.: Машиностроение, 1965.
3. Дьяков С..П. Об устойчивости ударных волн. ЖЭТФ, 27, 288-295, 1954.
4. Иорданский С.В. Об устойчивости плоской стационарной ударной волны. ПММ, 21, 465-472, 1957.
5. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988.
6. Егорушкин С.А., Успенский В.С. Влияние опережающего излучения на устойчивость сильных ударных волн в газах с произвольным уравнением состояния. Изв. АН СССР, МЖГ, 3, 125-133, 1990.
7. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, 1966.
8. Барышников А.С., Бедин А.П., Масленников В.Г., Мишин Г.И. О неустойчивости фронта головной ударной волны. Письма в ЖТФ, 5, 281-284, 1979.
9. Годунов С.К., Забродин А.В. и др. Численное решение многомерных задач газовой динамики. М.: Наука, 1966.
10. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. М.: Наука, 1982.
11. Harten A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49, 357-393, 1983.
12. Colella P., Woodward P.R. The piecewise parabolic method (PPM) for gas-dynamical simulations. J. Comput. Phys. 54, 174-201, 1984.
13. Григорян С.С. О движении и разрушении метеоритов в атмосферах планет. Космич. исслед. 17, 875-893, 1979.
14. Chyba C.F., Thomas P.J., Zahnle K.J. The 1908 Tunguska explosion: atmospheric disruption of a stony asteroid. Nature 361, 40-44, 1993.
15. Hills J.G., Goda M.P. The fragmentation of small asteroids in the atmosphere. Astron. J. 105, 1114-1144, 1993.
16. Lyne J.E., Tauber M., Fought R. An analytical model of the atmospheric entry of large meteors and its application to the Tunguska Event. J. Geophys. Res., 101, 23207-23212, 1996.