Из радиальности вывала леса и отсутствия осесимметрического (относительно траектории) полосового вывала леса (рис. 1) следует, что мощность баллистической волны меньше мощности взрывной волны и была недостаточна, чтобы произвести вывал леса. Поэтому в пределах всей области разрушений в тайге избыточное давление на фронте баллистической волны 
P
меньше избыточного давления на фронте взрывной волны PB.
Как уже отмечалось, избыточное давление на фронте ударной волны, которая начинает валить деревья, равно 0,1 — 0,14 кг/см2 [105, 107], тогда в любой точке в пределах всей области разрушений на земной поверхности избыточное давление на фронте баллистической волны не могло быть более 0,1 кг/см2, так как баллистическая волна вывала леса не производила.
Таким образом, для баллистической волны имеет место условие
P' <0,1 кг/см2, (9)
которое выполняется во всей области разрушений. Это условие можно использовать для оценки верхнего значения энергии баллистической волны Тунгусского космического тела. Однако для такой оценки, кроме значения давления на фронте волны, необходимо знать и минимальное расстояние от центра волны, на котором волна должна произвести максимальное действие.
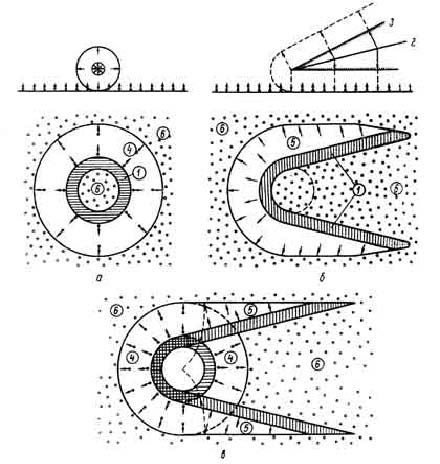Рис. 7. Положение зоны максимальных разрушений для сферического взрыва (а); для баллистической волны (б); для комбинированного вывала леса взрывной и баллистической волнами (в): 1 – зона максимальных разрушений; 2 – траектория космического тела; 3 – фронт баллистической волны; 4 – вывал леса взрывной волной; 5 – вывал леса баллистической волной; 6 – зона неповаленного леса
Так же, как и взрывная сферическая волна, баллистическая волна имеет зону максимального действия, которая расположена в области нерегулярного (трехударного) [108, 109] отражения баллистической волны от поверхности земли на расстоянии от проекции траектории, примерно равном высоте полета тела (рис. 7). В тунгусском случае при взрыве тела на высоте 5—-10 км минимальное расстояние от эпицентра до зоны максимального действия баллистической волны равно 7—14 км. Статистический анализ карты поваленного леса показывает, что даже в зоне максимального действия на минимальном расстоянии от конечного участка траектории, как и во всей области разрушений, баллистическая волна вывала леса не произвела (рис. 1, 4, 5), следовательно, неравенство (9) выполняется и для зоны максимального действия баллистической волны. Кроме того, следует учесть, что избыточное давление на фронте головной ударной волны, образующейся в области нерегулярного отражения в зоне максимального действия, не менее чем в два раза превышает избыточное давление на фронте прямой падающей волны [108, 109] (рис. 6). Поэтому для прямой баллистической волны в зоне максимального действия на расстоянии r2=(2H0)1/2 км (где H0— высота взрыва космического тела) от конечного участка траектории имеет место неравенство
P' <0,05 кг/см2, (10)
Таблица 2 Максимально возможные значения энергии баллистической волны при разной высоте взрыва Тунгусского космического тела
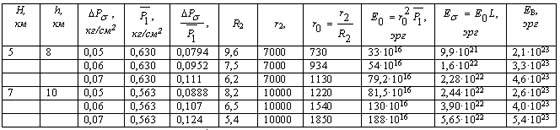
Примечание: E– энергия баллистической волны, EB – энергия взрыва
Известно, что движение ударной баллистической волны можно рассматривать по законам движения ударной волны цилиндрического взрыва [104]. Тогда давление на фронте прямой баллистической волны можно рассчитывать по формулам для цилиндрического взрыва, эквивалентного действию баллистической волны [104]:
; (11)
; (12)
(13)
где R'2— безразмерный параметр; r'2 — радиус ударной волны в м; r'0 — динамическая длина цилиндрического взрыва в м; E0 — энергия взрыва на единицу длины в кгм; 
— среднее значение давления в нижнем слое атмосферы толщиной, равной высоте взрыва, в кг/см2; 
— показатель адиабаты Пуассона; 
2 — постоянный множитель, для цилиндрического взрыва 2 = 0,983 [104].
По известному давлению на фронте баллистической волны в одной точке (условие (10)) согласно уравнениям (11) — (13), основные параметры волны однозначно определяются во всем пространстве. Так же, как и для взрывной сферической волны, изменение энергии баллистической волны с изменением высоты полета и взрыва космического тела учитывается через изменение с высотой среднего значения давления нижнего слоя атмосферы толщиной, равной высоте взрыва (табл. 2). Для сравнения в табл. 2 приводятся соответствующие значения энергии взрыва EB. Из табл. 2 следует, что максимально возможные значения энергии баллистической волны космического тела, выделившейся над областью разрушений (L = 30 км), в 10 раз меньше энергии тунгусского взрыва.