При достаточно большом количестве направлений поваленных деревьев как векторов центр совокупности этих векторов можно принять за центр разрушений. Однако при взрыве движущегося тела вследствие влияния баллистической волны, которое проявляется в искажении строгой радиальности вывала леса, центр совокупности векторов и эпицентр взрыва могут и не совпадать. Действительный эпицентр взрыва в сложных условиях тунгусского взрыва может оказаться на несколько километров впереди центра разрушений по направлению полета тела. В данном случае проведем анализ отклонений направлений поваленных деревьев относительно центра совокупности поля векторов, который получен методом наименьших квадратов и имеет координаты φ = 60°53'11"; λ=101°55'11", и относительно оси симметрии области разрушений, которая имеет азимут 294°±1° (рис. 1 и 16).
Анализ линейных отклонений r направлений поваленных деревьев от центра разрушений показал, что среднее квадратичное отклонение по оси симметрии области разрушений равно σх = 2,05 км, а по перпендикулярной оси σу=1,65 км (§ 12), т. е. среднее квадратичное линейное отклонение вдоль оси симметрии (проекции,траектории космического тела) заметно больше, чем по перпендикулярной оси:
2,05 км = σх>σу = 1,65 км. (38)
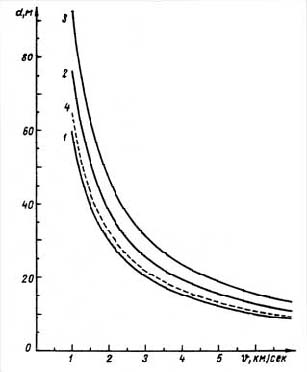Рис. 28. Зависимость диаметра космического тела от скорости при различной средней высоте полета над областью разрушений: l – h = 10 км, r2 = 25,5 км, CX = 0,92, ∆P = 0,005 кг/см2; 2 – соответственно 10; 25,5; 0,92; 0, 006; 3 – 10; 25,5; 0,92; 0, 007; 4 – 8; 24,7; 0,92; 0, 006
Это обстоятельство дает возможность оценить протяженность взрыва космического тела.
Допустим, что на высоте H0 = 5—7 км над лесным массивом произошел мощный сферический взрыв точечного заряда, который произвел радиальный вывал леса радиусом 25—30 км. Очевидно, что направления поваленных деревьев будут иметь некоторый разброс относительно эпицентра взрыва, который характеризуется средним квадратичным отклонением
σr2 = σх2 + σу2 (39)
Если рельеф окажется однородным, то средние квадратичные отклонения по двум взаимно перпендикулярным осям σх и σу будут равны
σх = σу (40)
Это условие характеризует сферическую симметрию взрыва.
Далее допустим, что на высоте 5—7 км над лесом произошел мощный цилиндрический взрыв линейного заряда длиной l=3—5 км, который произвел в общем радиальный вывал леса на расстоянии до 20—30 км. Однако в этом случае, по-видимому, будет наблюдаться некоторая осевая симметрия эпицентральной части вывала леса.
Среднее квадратичное отклонение направлений поваленных деревьев от эпицентра (эпицентром цилиндрического взрыва будет проекция центра линейного заряда) по координате X, направленной параллельно оси линейного заряда, будет равно
σх =0.5 l + σу (41)
где σу — среднее квадратичное отклонение по оси Y, направленной перпендикулярно оси линейного заряда. Тогда длину линейного заряда можно определить по формуле
l = 2 (σх - σу) (42)
Равенство (42) имеет смысл при условии
σх > σу, (43)
которое для воздушного протяженного взрыва имеет место тогда, когда высота взрыва не превышает нескольких значений (2—3) протяженности взрыва, т. е. в том случае, если при подходе к поверхности земли ударная волна протяженного взрыва еще не успеет выравняться в строго сферическую волну (из экспериментальных данных известно, что при цилиндрическом взрыве ударная волна выравнивается в сферическую волну на расстоянии нескольких длин цилиндрического заряда [118]). Тогда в области разрушений будет наблюдаться некоторое отклонение от строгой цилиндрической симметрии, вследствие чего появится некоторая осевая симметрия, при которой σх>σу.
Тунгусское космическое тело, по-видимому, взорвалось во время движения, поэтому естественно, что его взрыв имел некоторую протяженность вдоль траектории. Статистический анализ линейных отклонений r показал, что в тунгусском случае условие (43) выполняется (см. неравенство (38)), в связи с чем имеет место и равенство (42). Из равенства (42) следует, что при условии (43) протяженность взрыва не может быть больше удвоенного значения σх. Это условие можно использовать для оценки верхнего значения протяженности взрыва Тунгусского космического тела:
lT < 2σx = 4 км (44)
Можно получить более конкретную оценку протяженности тунгусского взрыва. Формула (42) справедлива для линейного заряда, для реального цилиндрического заряда формула (42) показывает разницу между длиной и диаметром d цилиндра. Поэтому длина цилиндрического заряда будет равна
lT = l + d=2(σx - σy) + d. (45)
Для полной совокупности всех n = 338 векторов имеем σх = 2,05 км, σу=1,65 км (ось X направлена вдоль проекции траектории космического тела), диаметр поперечного сечения тела равен 50—70 м (§ 17). Тогда протяженность взрыва космического тела lт=0,85 км. Но, по-видимому, более правильным будет расчет протяженности взрыва по данным совокупности векторов в зоне невозмущенного действия взрывной волны (секторы 19—36; 1—5, рис. 16). Для этой зоны σх=1,35 км, σу=1,1 км. Тогда протяженность взрыва космического тела lт = 570 м.
Таким образом, протяженность тунгусского взрыва почти на два порядка меньше размеров области разрушений, поэтому его можно считать практически единым центральным взрывом. Как уже отмечалось, вывод о центральном взрыве уже был сделан в литературе [86], в сущности такой вывод непосредственно следует из радиальности вывала леса, но конкретной оценки протяженности взрыва и анализа следствий этого вывода до сих пор не было сделано.
При малых размерах области взрыва по сравнению с областью разрушений к моменту подлета тела к области своего собственного взрыва независимо от его механизма и дальнейшего развития (будь то «быстрое взрывообразное испарение тела» по К.П. Станюковичу [69, 80] или «быстрое взрывообразное механическое разрушение тела» по Г.И. Покровскому [72], или «быстрое взрывообразное выравнивание баллистической волны облака космической пыли» по Г.Ф. Плеханову [86] и др.) еще до начала взрыва над областью разрушений (над проекцией конечного участка траектории) уже существовала баллистическая волна. На участке зоны разрушений вдоль проекции конечного отрезка траектории космического тела на поверхность земли баллистическая волна пришла раньше, чем взрывная волна. Тогда если мощность баллистической волны была достаточной для вывала леса, то она должна была его произвести. В этом случае при малом наклоне полета тела (β = 5—17° [38]) длина активного участка траектории L с точки зрения разрушений баллистической волной должна быть сравнима с размерами области вывала леса, т. е. L должна быть не менее 25—30 км. При малой протяженности тунгусского взрыва область разрушений делится на две части:
1. Область, в которой на поверхность земли баллистическая волна пришла раньше взрывной волны,— юго-восточная часть области вывала леса, расположенная вдоль конечного участка траектории (рис. 1).
2. Область, в которой, наоборот, взрывная волна пришла раньше баллистической волны,— северо-западная часть области разрушений (рис. 1). От места взрыва до границы области разрушений, т. е. в среднем на расстоянии 25 км, ударная волна взрыва распространяется в течение более 60 сек. Следовательно, в пределах области разрушений вдоль проекции траектории космического тела существуют участки, на которые баллистическая волна на несколько десятков секунд пришла раньше взрывной волны. При достаточной мощности баллистическая волна должна успеть повалить деревья на этих участках еще до прихода взрывной волны и образовать полосовой осесимметрический вывал леса. Причем эта полоса должна пересекать всю область разрушений вдоль траектории от края вывала леса до района эпицентра (рис. 3), чего не наблюдается в действительности (рис. 1).
Малая протяженность взрыва и отсутствие полосового вывала леса говорят о том, что, несмотря на существование к моменту взрыва баллистической волны на конечном участке пути над областью разрушений, она вывала леса не произвела. Однако до сих пор этот факт не учитывался ни в одном из предложенных вариантов взрыва Тунгусского космического тела [69, 72, 80, 86], в то время как на его основе, а также на основе анализа карты поваленного леса можно произвести количественную оценку параметров баллистической волны и космического тела.
Протяженность взрыва, по-видимому, можно принять за максимально возможную длину космического тела. Но если учесть, что взрыв тела произошел во время его движения, то действительная длина космического тела может быть значительно меньше протяженности взрыва (во сколько раз меньше — в несколько раз или на порядок,— зависит от скорости движения тела). Таким образом, длина Тунгусского космического тела независимо от его природы и структуры была не более 550—600 м.