О структуре и плотности Тунгусского космического тела было высказано несколько различных и противоречивых предположений. Одни авторы считают, что это было рыхлое снегообразное тело, другие в своих расчетах принимали космическое тело за монолитную глыбу из льда, камня или железа [69, 70]. Некоторыми авторами разрабатывается гипотеза о том, что Тунгусское космическое тело представляло собой рой частиц, составляющий голову кометы, или пылевое облако с объемной плотностью <<1 г/см3 и поперечным сечением в несколько квадратных километров [74, 86, 99]. По представлениям этих авторов получается, что плотность Тунгусского космического тела может иметь значения в пределах от 0,01— 0,001 г/см3 и менее, если считать, что тело было роем частиц или облаком космической пыли [86], до 1—8 г/см3, если принять, что тело было монолитной глыбой из льда или железа [69]. А размеры тела могут иметь значения от нескольких десятков метров, если это глыба [69], до нескольких сотен метров, если это рой частиц [74], и нескольких километров, если это облако пыли [86].
Таким образом, в зависимости от представлений различных авторов параметры Тунгусского космического тела произвольно могут меняться в пределах нескольких (3—4) порядков величины, и все это должно удовлетворять вполне определенным и конкретным условиям и следствиям Тунгусской катастрофы! (По-видимому, Тунгусское космическое тело имело более определенные параметры). Такую неопределенность в оценке параметров Тунгусского космического тела можно объяснить тем, что для определения этих параметров использовалась недостаточно полная система уравнений. Так, в работах [70, 80] для определения параметров космического тела, кроме уравнении метеорной физики, явно или неявно использовалось только одно соотношение (1), связывающее полную энергию ЕП, выделившуюся при катастрофе, конечные массу mк и скорость vk космического тела с его кинетической энергией Ек. Такой расчет основан на предположении, что все разрушения в тайге произведены за счет кинетической энергии двигавшегося тела.
Однако при одном определенном значении Ек конечные масса и скорость тела, удовлетворяющие уравнениям метеорной физики и условию (1), могут принимать целый интервал значений, отличающихся на порядок величины. Например, в работе [70] при значении Ек =1023 эрг конечная скорость тела имеет значения от 7 до 30 км/сек, а масса — от 2·104 до 8·105 т. И действительно, в зависимости от постановки задачи в разных работах принимаются различные значения массы и скорости Тунгусского космического тела, удовлетворяющие условию (1). Например, в работе [75] vk = 6 км/сек, mk =106 т, а в работе [69] для обоснования возможности так называемого «теплового взрыва» космического тела в воздухе конечная скорость тела принимается равной 30 км/сек, а масса — около 2·104 т.
Таким образом, для определения параметров космического тела одних уравнений метеорной физики и условия (1) оказалось недостаточно. Поэтому необходимы поиски новых независимых условий, связывающих конечные параметры космического тела. Например, для определения конкретных параметров космического тела дополнительно можно использовать связь скорости и размеров летящего тела при известной мощности баллистической волны, которую можно определить по фактическим данным о вывале леса в районе катастрофы.
В работе [71] дается приближенная оценка параметров Тунгусского космического тела, основанная на предположении, что все разрушения в тайге произведены только баллистической волной. Однако, как уже было показано в § 7, фактические данные о вывале леса в тайге не подтверждают этого предположения.
Конкретные параметры баллистической волны накладывают вполне определенные ограничения на размеры d и скорость v космического тела. Поэтому для оценки предельных значений параметров Тунгусского космического тела можно использовать верхнее значение мощности баллистической волны, определенное в § 9.
Имея в виду образование баллистической волны, космическое тело можно рассматривать как единое целое с определенными эффективными размерами независимо от природы и структуры тела. Поэтому если авторы работ [74, 80 и 86] считают, что рой частиц или облако космической пыли при полете в атмосфере образовало ударную баллистическую волну, то по мощности этой волны в принципе можно определить эффективные размеры dз роя частиц или облака пыли. И действительно, если, по мнению авторов работы [86], космическое тело как облако пыли могло образовать единую, общую для центрального сгустка (роя частиц) баллистическую волну, которая в результате резкого торможения «выравнялась» в сферическую волну и произвела все разрушения в тайге, то с точки зрения образования баллистической волны этот сгусток пыли должен иметь соответствующее эффективное поперечное сечение. А если же рой частиц был настолько редким, что каждая частица или пылинка при своем движении образовала отдельную самостоятельную баллистическую волну, то в этом случае не будет ни эффективных размеров тела, ни общей единой для всего роя баллистической волны.
Короче говоря, если какое-либо тело независимо от структуры (монолит или рой частиц) при сверхзвуковом полете в атмосфере образовало единую баллистическую волну, то оно имеет вполне определенное значение эффективного поперечного сечения, которое можно рассчитать по известным параметрам баллистической волны.
Связь между диаметром dз эффективного поперечного сечения тела, летящего со сверхзвуковой скоростью v и образующего баллистическую волну, и между характерным параметром эквивалентного цилиндрического взрыва r0 выражается следующей формулой:
, (14)
где Сх — коэффициент сопротивления; M =v/
— число Маха; — скорость звука в воздухе.
Из уравнений (11) — (14) следует, что величина динамической длины эквивалентного цилиндрического взрыва r0 полностью и однозначно характеризует параметры космического тела и баллистической волны, образуемой полетом этого тела в атмосфере.
Формула (14) показывает, что, определив характерный параметр эквивалентного цилиндрического взрыва r0 по данным обработки карты поваленного леса и задавая скорость космического тела, можно определить эффективный диаметр поперечного сечения Тунгусского космического тела.
В конкретных условиях Тунгусской катастрофы, описанных выше, для каждого значения скорости формулы (11) — (14) при условии (10) дают максимальные размеры тела (для случая шара — его эффективный диаметр). Максимальные значения диаметра поперечного сечения космического тела в зависимости от скорости его полета были рассчитаны по формулам (11) — (14) и условию (10) для минимального значения Сх = 0,92 (при скорости v>1 км/сек) и для трех значений высоты взрыва тела: H0 = 5; 7 и 10 км (рис. 8, кривые 1—3).
До сих пор мы не делали никаких предположений относительно механизма и характера тунгусского взрыва. Все оценки получены только на основании фактических данных о вывале леса и экспериментальных данных по крупным взрывам. Установленные конкретные параметры баллистической волны накладывают вполне определенные ограничения на размеры dэ и скорость v космического тела. Как уже отмечалось, с учетом образования баллистической волны космическое тело независимо от его природы и структуры можно рассматривать как единое целое с определенными эффективными размерами. Поэтому при рассмотрении любой гипотезы о тунгусском явлении, по-видимому, необходимо учитывать найденную зависимость между размерами Тунгусского космического тела и его скоростью (рис. 8, 1—3).
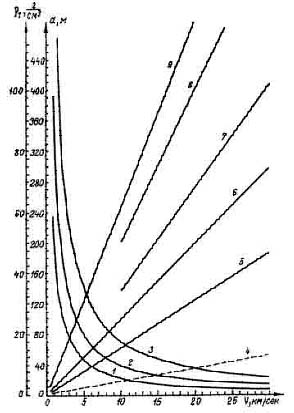Рис. 8. Зависимость диаметра (1-3) и плотности (4-9) космического тела от скорости при различной высоте гипотетического теплового взрыва этого тела: 1 – H = 5 км, r2 = 7 км, CX = 0,92; 2 – соответственно 7; 10; 0,92; 3 – 10; 14; 0,92; 4 - 10; 14; 0,92; Ek = 4 · 1023; 5 - 7; 10; 0,92; 2,5 · 1023; 6 - 7; 10; 0,92; 4 · 1023; 7 – 10; 14; 3,6; 4 · 1023; 8 - 7; 10; 2.0; 2,5 · 1023; 9 – 5; 7; 0,92; 2 · 1023
Например, если авторы [86] считают, что Тунгусское космическое тело имело скорость 10—50 км/сек, то даже при минимальной скорости v = 10 км/сек тело могло иметь диаметр эффективного поперечного сечения не более 70 м, а при скорости v = 50 км/сек — не более 14 м. Если бы тело имело большие размеры, то при этих скоростях оно образовало бы более мощную баллистическую волну, которая должна была бы произвести полосовой вывал леса, чего не наблюдается в действительности (рис. 1, 4 и 5). Но при размерах 14-70 м Тунгусское космическое тело облаком космической пыли или роем частиц, как предполагают авторы работы 186], по-видимому, быть не может.
Кривые 1—3 рис. 8 получены на основании фактического материала, они имеют объективное содержание, поэтому их необходимо учитывать при решении вопроса о возможной структуре Тунгусского космического тела и определении других параметров.
Теперь сделаем предположение о том, что взрыв космического тела и все разрушения в тайге произошли за счет кинетической энергии этого тела. Тогда будет иметь место соотношение (1). В этом случае из формул (11) — (14) и соотношения (1) найдем минимальные значения возможной плотности космического тела 
m:
, (15)
где и — средние значения давления и скорости звука в нижнем слое атмосферы толщиной, равной высоте взрыва Н0.
Кривые зависимости минимально возможной плотности космического тела от его скорости, вычисленные по формуле (15) и условию (10), рассчитаны для Н0 = 5; 7 и 10 км, r2 — соответственно 7; 10 и 14 км, для трех значений Сх = 0,92; 2 и 3,6 и трех минимальных значений энергии Еk — 2·1023; 2,5·1023 и 4·1023 эрг, соответствующих высоте взрыва 5; 7 и 10 км (рис. 8, кривые 4—9). Физический смысл кривых 4—9 на рис. 8 заключается в том, что, задавая определенную скорость космического тела, по формуле (1) находим необходимую массу и вкладываем ее в максимальные размеры тела, определенные по формуле (14), тогда по формуле (15) получаем минимально возможное значение плотности, соответствующее данной скорости этого тела.
Кривые 1—3 рис. 8 показывают максимально возможные размеры Тунгусского космического тела, а в предположении, что все разрушения в тайге произошли за счет кинетической энергии двигавшегося тела, кривые (4—9) показывают минимально возможные значения плотности космического тела в зависимости от скорости его полета. Поэтому кривые на рис. 8 дают возможность быстро и достаточно точно ориентироваться относительно параметров Тунгусского космического тела в рассуждениях при любых предположениях и гипотезах независимо от точки зрения исследователя на тунгусскую проблему. Кривые на рис. 8 переводят рассуждения относительно возможных значений параметров Тунгусского космического тела из неопределенности в несколько порядков в определенные рамки в пределах по крайней мере одного порядка величины. Рассмотрим несколько примеров.
Многие исследователи считают, что Тунгусское космическое тело летело с очень большой космической скоростью — в несколько десятков (30— 60) км/сек [39, 44, 58, 66, 69, 70, 74, 86]. Но при такой огромной скорости диаметр космического тела не может быть более 23 м (рис. 8, 3), а соответствующая плотность тела не может быть меньше 13 г/см3 (рис. 8, 4). Если при скорости 30 км/сек космическое тело будет иметь диаметр более 23 м, то оно вызовет более мощную баллистическую волну, которая при наклонном движении тела должна произвести полосовой осесим-метрический вывал леса, чего не наблюдается в действительности. Например, К.П. Станюкович считает, что над тунгусской тайгой произошел «тепловой взрыв» (быстрее испарение) ледяного тела, имевшего конечную скорость около 30 км/сек [69, 80]. Чтобы обеспечить запас кинетической энергии, необходимой для данных разрушений (4·1023 эрг), при скорости 30 км/сек масса тела должна составлять около 9·104 т. Ледяное тело шарообразной формы с плотностью около 1 г/см3 в этом случае должно иметь диаметр около 55 м. Если ледяное тело диаметром 55 м пролетит на высоте 7—10 км со скоростью 30 км/сек, то оно произведет полосовой вывал леса шириной около 100 км.
В настоящее время законы движения баллистической волны хорошо изучены, поэтому легко подсчитать мощность волны и размеры разрушений, произведенные баллистической волной, если в нижних слоях атмосферы пролетит тело диаметром в несколько десятков метров со скоростью нескольких десятков километров в секунду. Это можно рассчитать по формулам (11) — (13) и (14), можно рассчитать и по приближенной формуле М.А. Цикулина, которая признана Комитетом по метеоритам и опубликована в журнале «Метеоритика» [71]. Даже если принять, что все разрушения в тайге были вызваны только баллистической волной, то и в этом случае при скорости 30 км/сек космическое тело не должно иметь размеры более 30—35 м в диаметре [71].
Авторы работы [86] считают, что взрыв Тунгусского космического тела произошел на высоте 10—12 км с энергией около 1024 эрг [89], и допускают нижний предел скорости до 10 км/сек [86]. Но даже при такой малой (если иметь в виду взрыв тела в воздухе за счет кинетической энергии [69, 80]) скорости эффективный диаметр космического тела не мог быть более 50—70 м, а соответствующая плотность тела не могла быть менее 10 г/см3. При таких размерах и плотности Тунгусское космическое тело, по-видимому, не могло быть роем частиц или облаком космической пыли. Оно должно быть монолитным телом.
Если считать, что при малых поперечных размерах плотность тела может быть малой вследствие очень большой протяженности (до 20—30 км и более) роя частиц или облака пыли, то в этом случае будет невозможен малопротяженный сферический взрыв и невозможен радиальный вывал леса.
Таким образом, независимо от причины и характера взрыва, независимо от своей природы Тунгусское космическое тело должно быть компактным единым телом с эффективным диаметром не более нескольких десятков метров.
Рассмотрим дополнительно некоторые соображения о возможности пылевой структуры Тунгусского космического тела. Известно, что Тунгусское космическое тело проникло в плотные слои атмосферы и взорвалось в воздухе в пределах тропосферы [54] на высоте не менее 5 км [64, 86]. Поэтому возникает вопрос, может ли рой частиц или пылевое облако с объемной плотностью ρт<<1 г/см3 проникнуть в пределы тропосферы и как единое целое двигаться в плотных слоях атмосферы со скоростью несколько десятков километров в секунду. Задача о движении в атмосфере роя частиц или облака пыли с плотностью ρт<<1 г/см3 до сих пор еще не решена.
Выдвигая свою гипотезу о природе Тунгусского космического тела, Томская группа исследователей под руководством Г.Ф. Плеханова обычно ссылается на предположение, высказанное академиком В.И. Вернадским о том, что космическое тело представляло собой облако космической пыли [86]. Но здесь следует отметить, что В.И. Вернадский считал эту пыль химически активной [16, 23] (кстати сказать, в дальнейшем В.И. Вернадский на своем предположении не настаивал). Для объяснения химического взрыва облака космической пыли нет необходимости рассматривать задачу о движении этого облака в атмосфере. Тогда как для объяснения механизма нехимического взрыва облака космической пыли в воздухе за счет его кинетической энергии, как считает Томская группа, решение такой задачи необходимо. Авторы работы [86] не приводят никаких расчетов для обоснования своей «пылевой» гипотезы.
Однако некоторые вполне определенные выводы о движении облака космической пыли в атмосфере можно сделать и без расчета.
1. Авторы работы [86] считают, «что тело Тунгусского метеорита представляло рой частиц, расстояния между которыми в десятки и сотни раз превышали размеры самих частиц». Но при таких больших расстояниях между частицами каждая пылинка такого роя при входе в атмосферу с космической скоростью представит собой отдельное метеорное тело, будет двигаться в атмосфере самостоятельно и сгорит на высоте 80—100 км [101], образуя обычное метеорное явление. А весь рой в целом представит грандиозный метеорный поток и, по-видимому, сгорит на высоте в несколько десятков километров.
2. Движение в атмосфере роя частиц или облака космической пыли можно представить как движение струи. Известно, что струя быстро рассеивается и может существовать на расстояниях от точки истечения, не превышающих нескольких десятков диаметров струи. Длина пути Тунгусского космического тела в атмосфере по наклонной траектории равна около 700 км [38]. Диаметр Тунгусского космического тела как роя частиц должен быть равен нескольким сотням метров [35], по представлениям авторов работы [86], центральный сгусток космической пыли должен иметь диаметр несколько километров. При таких размерах облако космической пыли, по-видимому, не может пробить весь слой атмосферы по наклонной траектории, по какой летело Тунгусское космическое тело (β = 5—17° [38]), и не сможет достичь нижних слоев атмосферы.
Таким образом, даже качественное рассмотрение задачи вызывает вполне обоснованные сомнения в том, что Тунгусское космическое тело могло представлять собой рой частиц или облако космической пыли, которое могло бы «взорваться» за счет кинетической энергии.
Расчеты и выводы, сделанные в § 5, показывают, что, если предположить возможность пылевой структуры Тунгусского космического тела, мы неизбежно придем к дилемме:
1. Если считать, что космическое тело как рой частиц или облако пыли было достаточно плотным и могло образовать баллистическую волну, то имеется принципиальная возможность определить эффективные поперечные размеры тела. Расчеты показывают, что в этом случае диаметр тела должен быть не более нескольких десятков метров. Но при таких малых размерах тело не может быть роем частиц или облаком пыли. При условии, что тело разрушилось или взорвалось за счет кинетической энергии при таких размерах с необходимым весом около 105 т, Тунгусское космическое тело должно быть монолитным телом с плотностью не менее 10 г/см3.
2. Если космическое тело было очень сильно распыленным с большим расстоянием между частицами и оно не образовало единой баллистической волны, то в этом случае каждая частица сгорела бы в отдельности и тело бы не произвело в тайге никаких механических разрушений.
Итак, если космическое тело было настолько распыленным, что не могло образовать единую баллистическую волну, то оно не могло и произвести никаких разрушений в тайге (нет ударной волны — нет вывала леса). А если космическое тело могло образовать единую баллистическую волну и поэтому могло бы произвести разрушения в тайге, то оно по своим малым размерам в тунгусском случае не могло быть роем частиц или облаком пыли.
Таким образом, предположение о том, что Тунгусское космическое тело могло быть роем частиц или облаком космической пыли, не соответствует фактическим данным и его, по-видимому, можно исключить из дальнейшего рассмотрения.