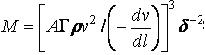Входящий в атмосферу с космической скоростью метеороид начинает взаимодействовать с атомами и молекулами атмосферы. На больших высотах (выше 120 км), где атмосфера разреженная, можно рассматривать удары о поверхность метеороида отдельных атомов и молекул воздуха. Эти удары (со скоростью, напомним, от 11 до 72 км/с) вызывают мгновенный разогрев небольших участков поверхности и испарение нескольких атомов вещества метеороида. В самом деле, сделаем небольшой расчет. Удельная (приходящаяся на 1 г вещества) энергия налетающей молекулы колеблется для указанного интервала скоростей от 6 1011 до 2,6 1013 эрг/г, тогда как для испарения метеорного вещества (безразлично, каменного или железного состава) требуется только 8 1010 эрг/г. Значит, энергии набегающей молекулы воздуха достаточно для испарения от 7 до 300 атомов метеороида (Этот расчет справедлив для случая равенства атомных (молекулярных) масс набегающей и испаряющейся частиц. В случае каменных тел это условие примерно выполняется.).
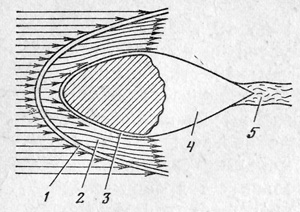
Но вот атмосфера становится плотнее, удары молекул воздуха — чаще. Ниже 120 км начинается новое явление: отскакивающие от поверхности метеороида молекулы воздуха сталкиваются с налетающими и преграждают им путь, не дают удариться о поверхность. Возникает эффект загораживания метеороида отлетающими молекулами (рис. 10).
По мере развития процесса испарения число испарившихся молекул метеороида уже заметно превышает число отлетающих. Начиная с этого момента основную роль в загораживании играют именно испаряющиеся молекулы.
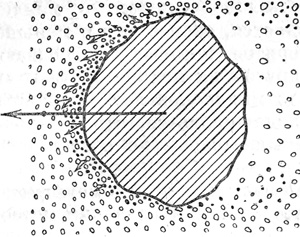
Рис. 10. Схема взаимодействия молекул с поверхностью метеороида. Молекулы воздуха показаны светлыми кружками; молекулы метеорных паров — темными. В нескольких случаях показаны их столкновения между собой
Как показал еще в 1956 г. советский исследователь метеоров Б. Ю. Левин, переход к интенсивному испарению происходит очень быстро, на диапазоне высот не более 1—2 км. Это связано с быстротой нагрева метеорной частицы ударами молекул воздуха.
Теперь два процесса — испарение и загораживание испарившимися молекулами — как бы регулируют друг друга. Чем сильнее испарение, тем больше загораживание, а значит, тем меньшая доля налетающих молекул может передать телу свою энергию, необходимую для поддержания испарения. Напротив, если испарение вдруг ослабеет, уменьшится и загораживание, а, значит к телу станет поступать больше энергии. Это вызовет усиление испарения. Лишь при одной какой-то скорости испарения оба процесса будут находиться в равновесии. Эта равновесная скорость испарения определяется внешними условиями: скоростью движения метеороида, его размерами (или массой), плотностью окружающего воздуха, составом и теплофизическими свойствами тела. В меньшей степени влияют угол входа в атмосферу и форма тела.
Интересно, как распределяется кинетическая энергия метеороида между ним самим, отлетающими и испаряющимися молекулами? На самом верхнем участке пути, до начала интенсивного испарения, примерно половина энергии уносится отлетающими молекулами, а половина «достается» телу, т. е. идет на его нагрев и испарение. Но по мере развития испарения испаряющиеся молекулы уносят львиную долю энергии метеороида. При скорости 15 км/с на участке интенсивного испарения на их долю приходится 60% всей энергии, при скорости 30 км/с — 89%, а при скорости 60 км/с —97% всей энергии! Отлетающие молекулы уносят соответственно 33,9 и 2,6% энергии, на испарение тела остается при тех же скоростях 7,2 и 0,4% энергии.
Энергетика крупного метеороида намного сложнее. Дело в том, что достаточно большое тело, входящее в атмосферу с космической скоростью, образует перед собой отсоединенную ударную волну — скачок уплотнения воздуха, на фронте которой резко изменяются свойства набегающего потока воздуха: резко возрастают давление, температура и плотность газа, но также скачком уменьшается скорость течения. С возникающими при этом явлениями мы познакомимся ниже.
Испарение или плавление?
Выше мы говорили об испарении наружного слоя метеороида. Однако возможен еще один процесс: расплавление наружного слоя и сдувание пленки расплава набегающим потоком воздуха. Какой же из этих двух процессов уноса массы метеороида преобладает, играет главную роль? Этот вопрос в течение многих лет был предметом острой дискуссии среди специалистов.
Некоторые исследователи метеоритов (в первую очередь Е. Л. Кринов) поддерживали концепцию плавления и сдувания. Для обоснования этой точки зрения они предъявляли фотографии поверхности некоторых метеоритов, на которых ясно заметны застывшие брызги и капли расплава (см. вкл.). Такую картину можно наблюдать, правда, только на поверхности железных метеоритов. Однако и железные, и каменные метеориты покрыты снаружи корой плавления, имеющей толщину от долей миллиметра до 1—2 мм. У железных метеоритов она меньше, у каменных — больше. Но ее присутствие означает, что плавление происходит и у тех, и у других.
Против концепции плавления и сдувания выступил известный исследователь метеоров Б. Ю. Левин. Не отрицая проявления этих факторов на заключительной стадии полета метеороидов в атмосфере, он привел ряд аргументов в пользу испарения как основного механизма уноса их массы.
Прежде всего, толщина пленки расплава на поверхности метеороида должна быть весьма мала (сотые доли сантиметра), значит, унос массы с этой пленкой не должен быть велик.
Известно, что удельная энергия плавления каменных и железных метеороидов (включая энергию, идущую на подогрев вещества до точки плавления) составляет 2 1010 эрг/г— в 4 раза меньше, чем удельная энергия испарения. Это значит, что при том же подводе энергии за счет плавления и последующего сдувания пленки расплава можно удалить за то же время вчетверо большую массу, чем за счет испарения.
Но различие в действии обоих механизмов уноса массы (или абляции, как принято называть этот процесс) состоит не только в этом. При интенсивном испарении впереди тела образуется плотный слой испарившихся молекул, который загораживает поверхность метеороида от набегающих молекул, о чем уже говорилось выше. Поэтому доля энергии потока, достигающая поверхности и идущая на испарение, может быть в несколько раз меньше, чем в случае, если происходит только плавление.
Оба фактора — различие удельных энергий абляции и загораживание испарившимися молекулами — действуют в одном направлении и приводят к тому, что в случае плавления и сдувания пути метеоров должны быть много короче, чем в случае испарения. Выпавшие на Землю метеориты должны составлять ничтожную долю тела, вошедшего в атмосферу Земли.
Аргументация Б. Ю. Левина против концепции плавления и сдувания была основана на логических соображениях и анализе немногих наблюдений метеоров (в основном визуальных), но она показалась большинству специалистов настолько убедительной, что почти все согласились с его точкой зрения на испарение как на основной механизм уноса массы метеорных тел.
Между тем запуск искусственных спутников Земли потребовал от ученых и инженеров точного решения этой задачи. Нужно было знать, какой слой покрытия того или иного состава будет унесен при возвращении спутника и его входе в плотные слои атмосферы.
Первое решение задачи об одновременном протекании испарения и плавления поверхности, обтекаемой быстрым (сверхзвуковым) потоком газа, предложил американский ученый Л. Роберте в 1959 г. Однако в 1961 г. советский исследователь Г. А. Тирский указал на ряд ошибок в решении Робертса и дал свой метод решения задачи. Правда, решение Г. А. Тирского было довольно сложным для повседневного практического применения.
Ничего не зная о работах Л. Робертса и Г. А. Тирского, исследователи метеоров искали собственные пути решения той же задачи. Группа американских астрономов во главе с А. Куком получила в 1963 г. приближенное решение задачи, из которого следовало, что железные метеороиды теряют почти всю массу за счет плавления и сдувания, а каменные — некоторую, но вполне заметную ее часть. Эта доля зависит от скорости метеороида и плотности атмосферы, а в меньшей степени — от его размеров. Чем больше скорость и плотность набегающего потока воздуха, тем больше доля массы, уносимая испарением.
В 1967 г. ту же задачу для мелких метеорных тел, способных проплавляться насквозь, решили В. Н. Лебединец и Ю. И. Портнягин. Их результаты также говорили в пользу значительной (а для железных тел — основной) роли плавления и сдувания в уносе массы. В 70-е годы эту концепцию развивали киевские астрономы В. Г. Кручиненко и А. Н. Шайдо.
Исследование этого вопроса, выполненное в 1980—1981 гг. автором этой книги (совместно с М. И. Тертицким), показало, что унос вещества в жидкой фазе у железных тел много больше (порой на один-два порядка), чем у каменных. Этого и следовало ожидать, поскольку вязкость железа в десятки раз меньше, чем у пород, из которых состоят каменные метеориты. Унос в жидкой фазе быстро растет с плотностью воздуха (т. е. по мере снижения метеороида), особенно у железных тел. У малых тел унос в жидкой фазе больше, чем у крупных. У железных тел унос в жидкой фазе быстро растет со скоростью, у каменных зависимость от скорости выражена слабее.
Унос вещества в газовой фазе (за счет испарения) растет с плотностью атмосферы и со скоростью тела. От размеров тела он зависит слабо. Различие скорости испарения для каменных и железных тел невелико.
Таким образом, далеко не вся масса метеорного тела уносится за счет испарения. У железных тел большая часть массы уносится путем сдувания расплавленной пленки, тут же дробящейся на мелкие капли, следы которых можно видеть на фото (см. вкл.). У каменных тел на больших высотах (~100 км) лишь 10—20% массы уносится за счет испарения, но на высоте 80 км эта доля возрастает до 50—100%. Еще ниже практически вся масса уносится путем испарения. Чем больше скорость метеороида, тем быстрее растет доля уноса испарением по мере внедрения метеороида во все более плотные слои атмосферы.
А есть еще и дробление
В середине 50-х годов американский исследователь метеорных явлений Л. Яккиа и советский ученый Б. Ю. Левин обратили внимание на ряд признаков, свидетельствующих о том, что метеорные тела в атмосфере испытывают дробление, дробятся на несколько (порой на много) отдельных осколков. Впоследствии тщательное исследование этого явления выполнила А. Н. Симоненко. Вот какие наблюдательные данные свидетельствуют о том, что метеорные тела действительно дробятся в полете:
1) траектории метеоров оказываются короче, а высоты погасания — выше, чем следует из классической теории испарения недробящихся тел той же массы;
2) больший блеск в максимуме, чем следует из классической теории;
3) различие между формой наблюденных и теоретических кривых блеска метеоров;
4) наличие на кривых блеска метеоров неправильных колебаний, быстрых подъемов блеска на разных участках траектории;
5) различие между значениями масс метеороидов, определенных по их торможению в атмосфере (динамическая масса) и по кривой блеска метеоров (фотометрическая масса);
6) разделение метеоров на несколько частей (фрагментов), наблюдаемое непосредственно на фотографиях, снятых по методу мгновенной экспозиции (см. рис. 11);
7) замывание перерывов на фотографиях, снятых с обтюратором (см. гл. I), особенно у слабых метеоров;
8) многочисленные факты дробления в воздухе достигающих поверхности Земли метеоритов.
Первые семь явлений обнаруживаются астрономическими методами, восьмое — непосредственным изучением метеоритных падений. Самым наглядным из астрономических свидетельств дробления являются, конечно, фотографии, полученные по методу мгновенной экспозиции (рис. 11), на которых непосредственно видно отделение крупных фрагментов. Но и на обычных фотографиях, особенно фотографиях ярких болидов, заметно отделение фрагментов, причем дробится не только главное тело, но и уже отделившиеся от него крупные фрагменты. Таким образом, дробление может быть прогрессивным: главное тело дробится на осколки первого поколения, те, в свою очередь,— на осколки второго поколения и так далее.
Рис. 11. Снимок метеора 8 августа 1965 г., сделанный по методу мгновенной экспозиции. В точке А' малый фрагмент начинает отставать от крупного, а перед точкой А" от него отделяется новый фрагмент (по П. Б. Бабаджанову и Е. Н. Крамеру)
Кроме этой формы дробления, прослеживаемой как на фотографиях метеоров, так и из анализа расположения мест падения индивидуальных экземпляров метеоритных дождей, большое значение имеет другая форма дробления — квазинепрерывное дробление, или шелушение. Оно представляет собой непрерывное отделение от главного тела множества мельчайших частиц размерами в доли миллиметра и мельче.
К каким же последствиям приводят разные формы дробления метеороидов? Для того чтобы ответить на этот вопрос, посмотрим, от чего зависят такие процессы, как торможение, абляция метеороидов в атмосфере и излучение порождаемых ими метеоров.
Торможение метеороидов в атмосфере
Еще в 30-е годы было точно установлено, что торможение метеороидов, влетающих в атмосферу с космическими скоростями, пропорционально квадрату их скорости. Почему это так, понять нетрудно. Набегающий поток молекул передает метеорному телу определенную долю своего импульса (количества движения). Если поперечное сечение (мидель) тела имеет площадь S, то за единицу времени на него набегает масса воздуха, равная S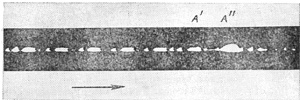
![]() v, где —
v, где —![]() плотность атмосферы, v— скорость метеорного тела (или, если хотите, скорость набегающего потока воздуха, если представить себе тело неподвижным). Количество движения этой массы будет равно ее произведению на скорость, т. е. S
плотность атмосферы, v— скорость метеорного тела (или, если хотите, скорость набегающего потока воздуха, если представить себе тело неподвижным). Количество движения этой массы будет равно ее произведению на скорость, т. е. S![]() v2. Пусть телу передается доля Г этой величины. Если оно имеет массу М, то оно приобретает импульс Mdv/dt, где dv/dt— уменьшение скорости тела в единицу времени (торможение). Приравнивая обе величины, получим уравнение торможения метеорного тела:
v2. Пусть телу передается доля Г этой величины. Если оно имеет массу М, то оно приобретает импульс Mdv/dt, где dv/dt— уменьшение скорости тела в единицу времени (торможение). Приравнивая обе величины, получим уравнение торможения метеорного тела:
Mdv/dt=-Г S![]() v2
v2
Знак минус означает, что скорость тела уменьшается, а не растет. Это уравнение — одно из основных уравнений физической теории метеоров.
Разделим теперь обе части уравнения на М. Получим формулу для определения торможения:
dv/dt=-Г (S/M)![]() v2
v2
Видно, что торможение тела пропорционально отношению S/M,характерному для данного тела. Но масса тела равна его объему V, помноженному на плотность :
M=V.
Отсюда следует, что интересующее нас отношение равно
S/M=S/V =A/M1/3
2/3
где через А мы обозначили величину S/V2/3, называемую коэффициентом формы. Легко подсчитать, что для куба (S=a2, V=a3) A = 1, для шара (S= В действительности форма метеороидов (если судить по форме падающих на Землю метеоритов) неправильная и не может быть известна заранее. Обычно полагают A=1,21 (как для шара). Если тело быстро вращается, это предположение недалеко от истины.
Теперь ясно, что торможение обратно пропорционально кубическому корню из массы тела и плотности в степени 2/3. Это значит, что более плотные железные тела тормозятся слабее, чем каменные, а плотные каменные — слабее, чем рыхлые. Массивные тела тормозятся слабее тел малой массы. Поэтому отделяющиеся от главного тела осколки будут тормозиться сильнее и отставать от главного тела. Это обстоятельство имеет большое значение. Именно из-за осколков, отстающих от главного тела, происходит замывание обтюраторных перерывов на фотографиях.
Из уравнения торможения многие исследователи пытались определять массу метеороидов. Полагая А = 1,21 и принимая плотность равной плотности каменных метеоритов (вспомним, что их подавляющее большинство), можно, определив по фотографиям, снятым через обтюратор, скорость и торможение метеора, найти его массу:
Плотность атмосферы берется из таблиц строения верхних слоев атмосферы, часто называемых моделью атмосферы. Нужно иметь в виду, что плотность и другие характеристики, выбираемые из модели, могут отличаться от реальных значений плотности и этих характеристик на данной высоте, в данном месте и в момент наблюдения. Но определить плотность независимым путем не представляется возможным.
Массы, определяемые описанным методом, называются динамическими.
В чем же недостаток динамического метода определения масс метеороидов? Казалось бы, его недостатки — это неточное знание коэффициента формы А (форма тела нам неизвестна), коэффициента сопротивления Г (обычно он заключен в пределах от 0,5 до 1), плотности воздуха Основной недостаток метода — невозможность учета дробления. В самом деле, если тело раздробилось на несколько осколков сравнимой массы, то впереди летит самый крупный осколок, за ним осколки поменьше, которые постепенно отстают от наибольшего осколка. Скорость и торможение, измеряемые по фотографии,— это параметры движения наибольшего осколка, и именно его массу, а не массу всего тела до дробления мы определяем описанным способом. Но какую долю общей массы составляет наибольший осколок, мы не знаем. Поэтому для надежного определения масс метеороидов динамический метод непригоден, хотя его использование порой представляет интерес для сравнения с другим методом — фотометрическим, который мы опишем ниже.
Абляция метеорного тела и излучение метеора
Мы уже рассказывали о различных формах абляции (потери массы) метеороидов. Выведем теперь уравнение потери массы. Подобно тому как торможение метеороида вызывается передачей ему импульса от набегающих молекул, так и абляция определяется передачей телу энергии от тех же молекул. Эта энергия равна потоку массы S Куда же расходуется получаемая телом энергия? Часть ее идет на нагревание тела от той температуры, которую оно имело в космическом пространстве, до температуры плавления.
Здесь мы должны обратить внимание читателей на одно очень распространенное заблуждение, связанное с представлением о так называемом холоде космического пространства. Большинство людей убеждены, что в космосе царят температуры, близкие к абсолютному нулю (—273° С). Наиболее ярко эта ошибочная точка зрения отражена в одном научно-фантастическом рассказе, где советская космонавтка Светлана спасает двух своих товарищей-космонавтов, изнемогших в борьбе с инопланетянами-луианами. Для этого Светлана открывает настежь люк космического корабля, в котором происходит схватка. В результате «холод космического пространства» мгновенно убивает незащищенных скафандрами луиан, но погибает и сама Светлана, оказавшаяся в этот момент без гермошлема. Ее товарищи, одетые в скафандры и гермошлемы, остаются живы.
Все это с научной точки зрения сплошной абсурд. Никакого космического холода не существует, и само понятие «температура космического пространства» лишено физического смысла. Речь может идти лишь о температуре того или иного тела, находящегося в космическом пространстве. Если говорить о метеороидах, то их температура (как и вообще всех тел, лишенных атмосферы) определяется притоком лучистой энергии от Солнца, их отражательной способностью (альбедо) и теплофизическими свойствами. Для быстро вращающегося тела без атмосферы средняя температура поверхности (в градусах Кельвина) равна
где А — альбедо, r — расстояние от Солнца в астрономических единицах. На расстоянии Земли r =1. Первый множитель мало отличается от единицы (даже для сравнительно светлых тел с А =0,2 он равен 0,95). Таким образом, средняя температура поверхности приближающихся к Земле метеороидов составляет 225—240 К.
На первом этапе нагревания метеороидов тепло, поступающее к нему от набегающих молекул воздуха, идет на повышение температуры его поверхности, а часть тепловой энергии метеороид сам отдает окружающему воздуху путем излучения. Если делать расчет получаемой и расходуемой энергии на единицу поверхности метеороида, то окажется, что отдача тепла излучением не зависит от радиуса тела, тогда как тепло, расходуемое на нагревание, пропорционально радиусу тела. Это и понятно, потому что приход тепла от набегающих молекул и расход на излучение пропорциональны поверхности тела, а расход на нагревание — его объему. Поэтому у малых тел будет преобладать отдача тепла излучением, а у более крупных — расход тепла на нагревание.
Но самые мельчайшие тела (по предложению американского астронома Ф. Уиппла, доказавшего в 1950 г. их существование, их называют микрометеороидами) успевают затормозиться в атмосфере до того, как начнут плавиться. Иначе говоря, они не достигнут температуры плавления. Почему это так, мы поймем, вспомнив, что торможение обратно пропорционально кубическому корню из массы частицы, т. е. ее радиусу, тогда как затрата энергии на нагревание, напротив, прямо пропорциональна радиусу. Как показывают расчеты, верхний предел радиуса микрометеороидов примерно обратно пропорционален кубу скорости и для железных частиц в 2,7 раза меньше, чем для каменных. Для каменных частиц, имеющих скорость 30 км/с, он равен примерно 5 мкм, если же скорость частицы превосходит 50 км/с, он становится меньше 1 мкм.
Микромотеороиды, затормозившись в атмосфере, дальше медленно оседают в ней, достигая поверхности Земли в зависимости от размеров за несколько часов или суток, а самые маленькие — примерно за месяц. Их можно обнаружить в ледниках, в снегах горных и полярных районов, в глубоководных отложениях (илах) на дне океанов, в слоях торфяников в тайге. Распределение их по слоям отложений льда, снега, ила или торфа может многое рассказать о притоке метеорной материи на Землю за многолетние интервалы времени.
Мелкие метеороиды основную долю получаемого ими тепла отдают за счет излучения. Нижний предел размеров этого класса тел равен верхнему пределу размеров микрометеороидов (1—5 мкм), верхний же предел составляет десятки или немногие сотни микрометров. Так, у каменных частиц, летящих со скоростью 30 км/с, этот предел равен 170 мкм, у железных частиц он примерно вдвое меньше и изменяется обратно пропорционально скорости частицы.
У средних частиц, размеры которых заключены в пределах от сотых (для быстрых частиц — тысячных) до десятых долей сантиметра, основная доля тепла идет на прогрев, причем эти частицы прогреваются (а затем и плавятся) насквозь, до самой середины. Еще более крупные частицы прогреваются уже не насквозь, а лишь в сравнительно тонком поверхностном слое.
Назовем глубиной прогрева крупных частиц глубину, на которой температура уменьшается в е раз (е=2,718...). При скоростях метеороида 15—60 км/с она равна 0,05— 0,03 см для каменных тел и 0,17—0,09 см для железных (меньшие значения реализуются при больших скоростях). Таким образом, температура тела с глубиной убывает постепенно.
Когда температура поверхности тела достигает температуры плавления, она начинает плавиться, а затем и испаряться. Одновременно может происходить и квазинепрерывное дробление (шелушение). На этом участке траектории большая часть энергии, получаемая телом от встречных молекул воздуха, расходуется именно на абляцию во всех ее формах.
Отделяющиеся от метеорного тела твердые частички и капельки расплава, попадая в поток набегающего воздуха, вскоре также испаряются. Но при этом они успевают немного отстать от главного тела. Таким образом, независимо от того, уносится масса метеороида в ходе чистого испарения или кипения расплавленной пленки, путем отделения жидких капель или твердых частиц, вся унесенная масса превращается в пар, который смешивается с набегающим потоком воздуха. Газовая подушка, образующаяся перед метеороидом и состоящая из смеси воздуха и метеорных паров, называется метеорной комой. В результате столкновений метеорных атомов с молекулами и атомами воздуха происходит разогревание метеорной комы до температур от 4 до 15 тысяч градусов, возбуждение метеорных атомов и их ионизация.
Возбужденные атомы и ионы высвечивают, излучая присущие им спектральные линии. Именно это излучение метеорных паров (а не свечение раскаленного твердого тела метеороида) и создает то явление, которое мы наблюдаем в виде метеора. Прямым доказательством этого являются спектры метеоров, состоящие исключительно из линий излучения атомов и ионов и полос излучения некоторых молекул. Газы воздуха (азот и кислород) тоже излучают спектральные линии, но их излучение составляет не более 3% общего излучения метеора. Признаков непрерывного излучения в спектрах метеоров и даже очень ярких болидов не обнаружено. Другое доказательство слабого вклада излучения твердого тела метеороида в общее излучение метеора мы дадим ниже.
Поскольку основной вклад в излучение метеора дает свечение его паров, можно определить массу метеороида по его излучению в любой точке траектории. Вот основы этого метода.
Пусть скорость испарения метеороида равна dM/dt. Сюда можно включить все формы потери массы, поскольку и жидкие капельки, и твердые частички, как уже говорилось, тут же испаряются, добавляя свою долю в общее излучение паров метеороида. Поэтому фотометрический метод в отличие от динамического дает нам общую массу метеороида независимо от процессов дробления и сдувания капель расплава.
В соответствии со сказанным выше уравнение потери массы будет выглядеть так:
dM/dt= — где Q — удельная энергия абляции, т. е. энергия, расходуемая на унос единицы массы тела.
Энергия испарившихся газов в расчете на единицу массы равна v2/2. Пусть в энергию излучения переходит доля t общей энергии. Тогда интенсивность излучения метеора будет равна
Подставляя в это уравнение излучения значение dM/dt из уравнения потери массы, будем иметь
Таким образом, излучение метеора пропорционально пятой степени его скорости. Однако этим зависимость интенсивности излучения метеора от скорости не исчерпывается, потому что коэффициент эффективности излучения Но как именно? В 50-е и начале 60-х годов большое распространение получила точка зрения, согласно которой коэффициент Но уже в середине 50-х годов известный исследователь метеоров Э. Эпик на основании теоретических соображений доказал, что зависимость В модели Эпика коэффициент Зная коэффициент Сравнение фотометрических масс с динамическими показывает, что первые всегда или равны вторым, или больше их. Как мы уже объясняли, это связано с эффектом дробления:: фотометрический метод дает массу тела в целом, вместе с отделившимися осколками, а динамический метод дает лишь массу наибольшего осколка.
Фотометрический метод широко используется для определения масс метеороидов. Разумеется, для его применения необходимо иметь корреспондирующую пару фотографий, одна из которых снята через обтюратор, чтобы иметь возможность определить скорость и высоту метеора в каждой точке, а также наклон траектории к горизонту. Кривая блеска снимается со второй фотографии (полученной без обтюратора).
Переход от модели А к модели В потребовал внесения изменений в шкалу метеорных масс. Наиболее обстоятельное исследование в этой области принадлежит И. Н. Ковшуну.
Теперь сравним излучение метеорных паров и самого твердого тела метеороида. Допустим, что мы наблюдаем метеор нулевой звездной величины, летящий на высоте 80 км со скоростью 30 км/с на расстоянии 100 км от нас. По таблицам И. Н. Ковшуна находим его массу 0,17 г. Если он каменный, то его объем равен 0,06 см3, радиус 0,25 см, поверхность миделя 0,2 см2. С расстояния 100 км «диск» такого метеороида будет виден под углом dM= =0,01". Пусть его поверхность раскалена до температуры ТM = 2000 К. Сравним его звездную величину mм со звездной величиной Солнца m где индекс «м» соответствует метеороиду, а индекс Итак, раскаленная поверхность метеороида дала бы в тех же условиях метеор слабее четвертой величины; ее свечение примерно в 50 раз слабее, чем свечение паров того же метеороида, cоответствующее метеору нулевой звездной величины (Напомним, что разность в 1 звездную величину соответствует отношению блеска в 2,5 раза, разность в 5 величин — отношению блеска в 100 раз.).
Вернемся к вопросу о причинах различия фотометрических и динамических масс метеороидов. Кроме объяснения его эффектом дробления, существовало еще одно объяснение. До сих пор во всех расчетах предполагалось, что по крайней мере каменные метеорные тела имеют ту же плотность, что и каменные метеориты (3 г/см3 и, во всяком случае, не меньше 2 г/см3). Но ведь метеорные тела — осколки или остатки разрушившихся комет, а ядра комет, по современным представлениям,— это ледяные конгломераты с вкраплениями твердых частиц метеорного состава (Недавние прямые исследования ядра кометы Галлея двумя советскими межпланетными станциями «Вега», а также зарубежными аппаратами «Джотто» и «Планета-А» не изменили наших представлений о природе кометных ядер. Ядро кометы Галлея оказалось неправильной формы: 15 км в длину и 8 км в ширину — с толстым слоем пыли, покрывавшей ледяное ядро). Таким образом, в составе метеорных тел, кроме минералов, входящих в состав метеоритов, могут присутствовать льды, наблюдающиеся в кометных ядрах (в основном обычный водяной лед Н2О с небольшими примесями СО2 и других молекул). Тогда средняя плотность метеорных частиц может быть и гораздо ниже характерной для метеоритов и приближаться к 1 г/см3.
Есть, однако, и другая причина существования космических частиц значительно меньшей плотности. По предположению Эпика, в космическом пространстве пылинки могут слипаться, образуя так называемые пылевые комочки. Эти весьма рыхлые образования могут иметь плотность значительно ниже 1 г/см3. В том, что такие сростки частиц действительно существуют, нас убеждают эксперименты по сбору космических частиц специальными ловушками, установленными на космических аппаратах. Пример одной из таких частиц показан на рис. 12.
Рис. 12. Космическая частица размером около 1 мкм, уловленная в стратосфере
Существование в метеорных телах пор, внутренних каверн также понижает их эффективную (объемную) плотность. Приходится, таким образом, различать минералогическую и объемную плотности метеороидов. Некоторые ученые (З. Цеплеха в Чехословакии, В. В. Бенюх в СССР) предлагали остроумные способы получить эти плотности раздельно, но в каждом из этих способов есть свои «подводные камни», затрудняющие их применение.
Как же сделать выбор между концепцией дробления и гипотезой «пылевых комочков» или иных форм частиц сверхнизкой плотности (порядка десятых долей грамма на кубический сантиметр) ? Здесь нужно заметить следующее.
В том, что дробление в различных формах действительно происходит, сомневаться не приходится: мы уже приводили выше целых восемь доказательств или признаков этого. Но это отнюдь не исключает гипотезу «пылевых комочков». Кроме частиц, захваченных ловушками космических аппаратов (см. рис. 12), в пользу этой гипотезы говорит и кометное происхождение метеорных тел, и такое простое соображение, что рыхлые частицы типа «пылевых комочков» должны сильнее дробиться. Ниже мы приведем еще одно довольно веское доказательство преобладания среди метеороидов, входящих в земную атмосферу, малоплотных тел.
Спектры метеоров
Спектральный анализ имел и имеет громадное значение в астрофизике. По спектрам самосветящихся небесных тел (звезд, туманностей, комет, Солнца) можно определять их состав, температуру, степень ионизации, наличие и напряженность магнитных полей, характер движения тела как целого и атомов и молекул в его наружных слоях. Первые спектры метеоров были сфотографированы на рубеже XIX и XX столетий. Самый первый спектр был снят случайно на обсерватории в Ареквипе (Перу) в 1897 г. Три следующих спектра получил астроном Московской обсерватории С. Н. Блажко (позднее член-корреспондент АН СССР) в 1904-1907 гг. Начиная с 30-х годов в нашей стране проводится систематическое фотографирование метеорных спектров. В этой работе наряду со специалистами принимают участие и любители астрономии. Большое число хороших спектров метеоров получили астрономы П. Миллман и Я. Холлидей в Канаде, З. Цеплеха в ЧССР, Е. Н. Крамер, X. Д. Гульмедов, П. Б. Бабаджанов и их сотрудники в СССР, Дж. Рессел в США, К. Нагасава в Японии. На долю этих пяти стран приходится почти 99% всех спектров метеоров, полученных в мире (рис. 13).
Рис. 13. Спектр яркого метеора со вспышкой. Метеор летит слева направо (по Я. Холлидею)
Однако по объему приносимой информации метеорная спектроскопия намного отстала от звездной. Первое время астрономы занимались только отождествлением спектральных линий и полос и установлением того, какие элементы и в каком состоянии высвечивают в метеорных парах. За восемь десятилетий в нескольких тысячах метеорных спектров было установлено присутствие линий следующих химических элементов:
1) нейтральные атомы: FeI (329), CrI (65), NiI (54), CoI (48), TiI (38), OI (32), CaI (27), NI (18),MnI (18), MgI (12), NaI (11), CI (6), SiI (5),BaI (2?), HI(1), AlI (1), LiI(l?), KI (1?), SrI (1?), MoI(1?)
2) однократные ионы: FeII (23), OII (17), NII (16), AlII (12), CrII (8), SiII (5), CaII(4), MgII (4), TiII (2), SrII (1?), BaII (1?);
3) молекулы: N2, CN, FeO, C2, CH, MgO;
4) молекулярный ион: N2+.
В скобках после обозначения каждого атома или иона указано число отождествленных мультиплетов (чаще всего отстоящих пар или троек линий, хотя мультиплет может состоять из одной или большего числа линий, чем три). Вопросительный знак означает, что отождествление линий данного элемента или иона пока еще ненадежно. Молекулы расположены в порядке интенсивности их излучения. Это не относится к атомам и ионам, так как большое число линий еще не обеспечивает сильного излучения. Напротив, иногда одна или две яркие линии вносят больший вклад в излучение, чем множество слабых. Так, очень интенсивен дублет Н и К ионизованного кальция (длины волн 3934 и 3968 А). На фотографии спектра метеора 12 августа 1934 г., полученной под Москвой П. П. Станюковичем, Г. О. Затейщиковым и И Е Васильевым, ясно виден дублет CaII на протяжении большей части пути метеора. Лишь в конце, в яркой вспышке проявилось еще 46 спектральных линий.
Очень ярким в метеорных спектрах бывает желтый дублет натрия 5890-5896 А. В некоторых спектрах он дает больше излучения, чем все другие линии. Также весьма ярок бывает зеленый триплет магния.
С другой стороны, железо хотя и не имеет таких ярких линий, но зато в его спектре содержится много средних и слабых линий, так что суммарное излучение железа порой превалирует над излучением других элементов Иногда наблюдаются чисто «железные» спектры состоящие из линий железа, его иона Fe II, окиси железа FeO и неизменных спутников железа - никеля и кобальта. В этих случаях можно с уверенностью говорить что мы наблюдали спектр «железного» метеора, связанного с влетом в атмосферу железного (без кавычек) метеороида.'
Но в спектрах большинства метеоров и болидов присутствуют линии многих элементов и полосы простейших соединений, перечисленных выше. Здесь мы, очевидно имеем дело с каменными метеороидами.
Линии и полосы азота и его соединений (NI, NII N2, N2+, CN) принадлежат атмосферному азоту, поскольку в состав метеоритов азот входит в ничтожном количестве Что касается кислорода, то тут дело сложнее, поскольку этот элемент присутствует и в атмосфере, и в составе метеоритов. Можно полагать, что примерно 50% высвечивающего кислорода атмосферного и 50% метеорного происхождения.
Не приходится удивляться тому, что самые яркие линии в метеорных спектрах принадлежат металлам: натрию, магнию, ионизованному кальцию. У атомов этих металлов низкие потенциалы возбуждения. Поэтому при столкновениях с набегающими молекулами или атомами воздуха именно атомы металлов возбуждаются в первую очередь: для их возбуждения нужна не очень большая энергия. Возбужденный атом вскоре отдает полученную в процессе возбуждения энергию в виде кванта излучения. Мы наблюдаем суммарное излучение многих атомов в виде серии ярких линий. Каждая линия соответствует определенному переходу электрона в атоме с возбужденного уровня на нижележащий (не обязательно на основной уровень или на тот, с которого произошло возбуждение) .
Чем выше температура в газе, тем большее число атомов находится в возбужденном состоянии, тем все более и более высокие энергетические уровни «заселены» электронами. Это соотношение определяется законом Больцмана. В условиях высоких температур создаются и более благоприятные условия для ионизации атомов, иначе говоря, для отрыва от них внешних электронов и образования положительных ионов. Мы уже видели выше, что в метеорных спектрах наблюдаются линии 11 атомарных ионов.
Но в метеорной коме условия несколько отличаются от условий в обычном сильно нагретом газе. Набегающие атомы и молекулы воздуха несут большую энергию. Ведь их скорость относительно атомов метеорной комы равна скорости метеора, т. е. десяткам километров в секунду. Энергия удара такой частицы уже при скорости 27 км/с достигает 100 эВ и растет пропорционально квадрату скорости. Но после первого столкновения набегающая частица теряет большую часть своей скорости, а после двух-трех столкновений ее скорость становится тепловой, соответствующей температуре комы.
Можно ли по спектру метеора получить информацию о физических условиях, царящих в коме? Оказывается, можно. Чехословацкий астроном З. Цеплеха применил к анализу метеорных спектров метод кривых роста, широко употребляемый в звездной спектроскопии. Метод этот состоит в следующем.
Рассмотрим некоторый объем газа, излучающий интересующую нас спектральную линию, и проследим, как будет изменяться ее интенсивность по мере увеличения числа атомов в данном объеме, возбужденных до верхнего уровня k, переход с которого приводит к высвечиванию данной линии. Пока оптический слой газа тонкий, интенсивность линии будет прямо пропорциональна числу излучающих атомов. Этот первый участок кривой роста проходит вдоль биссектрисы угла между осями координат (рис. 14).
Рис. 14. Кривая роста, построенная по интенсивностям линий железа в спектре яркого метеора (по З. Цеппехе)
По вертикальной оси отложены относительные интенсивности спектральных линий; по горизонтальной — величина, пропорциональная числу излучающих атомов. Масштаб — логарифмический. Прямая 1 показывает, как легли бы точки при отсутствии самопоглощения и затухания излучения
По мере роста числа атомов одни атомы начинают заметно поглощать излучение других и рост интенсивности линии замедляется. Это явление называется самопоглощением. Теперь рост интенсивности линии определяется в основном ее расширением за счет эффекта Доплера, связанного с тепловыми движениями атомов в метеорной коме. С дальнейшим ростом оптической толщи излучающего газа основную роль в расширении линий начинает играть уже не эффект Доплера, а затухание излучения в результате столкновений атомов между собой. Рост интенсивности линий снова ускоряется, хотя и не до такой степени, как на первом участке. Форма кривой роста зависит от температуры газа. Впрочем, надо оговориться, о какой именно температуре здесь идет речь. Когда мы имеем дело с раскаленным разреженным газом, значения температуры, определяемые на основании различных законов природы, оказывается, не равны друг другу. В таком случае говорят, что газ не находится в состоянии термодинамического равновесия.
Из спектров метеоров можно определить так называемую температуру возбуждения, входящую как параметр в закон Больцмана. Ее и определяют по кривой роста. При этом кривые роста приходится строить для каждого элемента отдельно. Это сравнительно легко для железа, у которого много мультиплетов, но порой затруднительно для других элементов. Поэтому применяют и другие методы определения температуры возбуждения, например по отношению интенсивностей спектральных линий с различными потенциалами возбуждения верхнего уровня.
Какие же температуры получаются для метеорной комы? З. Цеплеха по нескольким спектрам ярких болидов определил температуру возбуждения для железа от 3000 до 4000 К, для натрия — 4120, для кальция — 5280, для кислорода — 14 000 К. Японский астроном К. Нагасава получил для железа по двум спектрам в среднем 3190 К, американский исследователь Г. Харви для магния - 3250 К.
Приведенные значения дают нам представление о физических условиях в метеорной коме, о царящих там температурах. Мы видим, что они ненамного превышают температуру испарения железа и других металлов, которая в зависимости от давления набегающего потока воздуха может быть от 2400 до 3500 К (на метеорных высотах).
Различие температур для разных химических элементов и даже для разных групп мультиплетов железа показывает, кроме того, что в метеорной коме не реализуется термодинамическое равновесие и не осуществляется больцмановское распределение электронов по уровням с единой температурой. Неравновесность заселенности уровней и изменения ее вдоль пути метеора были установлены в 1978 г. советскими астрономами И. Н. Ковшуном и В. А. Смирновым.
А можно ли по спектру определить не только качественный химический состав испаряющихся метеороидов, т. е. набор атомов и молекул, который мы уже приводили, но и их количественный состав — процентное соотношение между веществами, входящими в состав метеороида. На первый взгляд это нетрудно сделать по интенсивности излучения отдельных элементов в линиях. Но в действительности дело обстоит гораздо сложнее. Интенсивность излучения в линиях, как мы уже убедились при анализе кривой роста, зависит не только от количества излучающих атомов, но и от потенциала возбуждения верхнего уровня, температуры газа, его оптической толщи, расширения линий, определяемого эффектом Доплера (тепловыми движениями атомов) и столкновениями атомов между собой.
Тем не менее астрономам удалось в ряде работ преодолеть указанные трудности и получить оценки состава ряда метеороидов по спектрам наблюдавшихся метеоров. Подобное исследование выполнил известный канадский исследователь метеоров П. Миллман по спектрам 10 ярких метеоров из метеорного дождя Драконид 9 октября 1946 г. Он использовал коэффициенты эффективности излучения для ярких мультиплетов натрия, кальция, магния и группы мультиплетов железа, полученные экспериментально на лабораторных установках двумя группами американских физиков. Это дало ему возможность перейти от интенсивностей излучения этих элементов непосредственно к количеству излучающих атомов.
З. Цеплеха в ряде работ, используя первый (прямолинейный) участок кривой роста для железа и приняв некоторые предположения в отношении других элементов, оценил концентрации девяти элементов в метеорной коме. Аналогичные исследования выполнили американский астроном Г. Харви и японский ученый К. Нагасава. Оказалось, что в большинстве случаев спектральный метод дает удовлетворительное согласие с лабораторными определениями химического состава каменных метеоритов — хондритов. В этом можно убедиться, рассмотрев табл. 3, в которой приведены логарифмы отношений концентрации ряда элементов к концентрации железа.
Для метеоритов приведены два крайних значения, соответствующих различным подклассам хондритов. Однако эти значения — усредненные для данного подкласса, если же взять определения концентраций элементов в отдельных метеоритах, разброс их значений будет гораздо больше.
Какие же выводы можно сделать? Концентрации кальция (относительно железа) по всем определениям полностью укладываются в интервал лабораторных значений для хондритов. Для магния значения Цеплехи, Харви (1971 г.) и Миллмана близки к нижнему пределу для хондритов, но оценки Харви (1970 г.) и особенно Нагасавы дают превышение по сравнению с хондритами; у первого примерно вдвое, у второго — в 10 раз. Превышение в 1,5—2 раза наблюдается для никеля. Оценки содержания натрия Харви и Миллмана близки к лабораторным, но у Нагасавы и особенно у Цеплехи получаются заниженные значения: примерно в 5 раз у первого и в 30 раз у второго. Содержание марганца ниже лабораторного по данным Цеплехи в 5 раз, а по данным Нагасавы — в 40 раз.
Таблица 3. Значения логарифмов отношений концентраций элементов к концентрации железа в метеорах и метеоритах, полученные разными авторами
Автор
Год Элемент кальций магний марганец никель натрий Метеоры З. Цеплеха 1964 -1.19 -0.30 -2.76 -0.98 -3.13 Г. Харви 1970 -1.28 0.13 - - -1.92
1971 -1.18 -0.30 - -1.00 -1.48 К.Нагасава 1978 - 0.80 -3.67 - -2.37 П. Миллман 1972 -1.37 -0.32 - - -1.37 Метеориты (хондриты) Б. Мэйсон 1971 -1.36 -0.29 -2.23 -1.35 -1.86
-1.17 -0.12 -1.90 -1.22 -1.48
Эти различия могут быть и реальными, и основанными на тех или иных ошибках или неточностях примененной методики. Мы ведь говорили уже, что метеороиды, наблюдаемые нами в виде метеоров, отличны по своему происхождению от метеоритов. А это значит, что у них может быть и иной химический состав. Обратимся, однако, к другому сравнительному исследованию состава кометных метеороидов и каменных метеоритов, которое провел советский исследователь метеоритов А. А. Явнель. Он нанес на диаграмму (рис. 15) отношения концентраций: Na/Mg и Fe/Mg для различных типов хондритов — обыкновенных (Н, L, LL) и углистых (CI, СII, СIII), а затем на ту же диаграмму нанес точку D, соответствующую отношениям тех же элементов для Драконид, по П. Миллману. Мы видим, что точка D легла как бы на продолжение последовательности СIII—CII-CI.
Автор этой книги продолжил исследование А. А. Явнеля, нанеся на ту же диаграмму точку Р для метеоров потока Персеид (по данным Миллмана) и точку N для различных метеоров (по данным Харви). Первая из них оказалась вблизи точки СIII, вторая — вблизи точки CI. Таким образом, кометные метеороиды близки по своему химическому составу (по крайней мере по соотношению содержания натрия, магния и железа) к углистым хондритам.
Методы количественного анализа метеорных спектров в сочетании с лабораторными экспериментами сулят большие перспективы. Для примера возьмем такой распространенный в каменных метеоритах минерал, как оливин. Он составляет от 25 до 60% вещества обыкновенных хондритов, 45-70% вещества палласитов (класс железокаменных метеоритов), 50-60% вещества уреилитов (один из классов ахондритов), входит в значительных количествах в состав углистых хондритов типов СII и СIII. Химическая формула оливина (Fe, Mg)2SiO4. Это значит, что в оливине присутствуют два минерала: фаялит Fe2SiO4 и форстерит Mg2SiO4 в виде смеси кристаллических зерен. Соотношение между ними в различных метеоритах разное - от чистого фаялита до чистого форстерита. По-видимому, в кометных метеороидах имеет место то же самое.
Теперь возьмем ряд образцов оливина с постепенным переходом от чистого фаялита к чистому форстериту так чтобы соотношение Fe/Mg в образцах было 0 : 10, 1 : 9, 2:8 и т. д. до 10:0. Растолчем образцы в порошок и получим спектры свечения этих порошков в пламени электрической дуги. Измерим в спектрах отношения интенсивностей избранных линий железа и магния и нанесем их на график в функции реального соотношения Fe/Mg. Мы получим некоторую калибровочную кривую, с помощью которой сможем по наблюдаемой интенсивности линий этих элементов судить о реальном отношении их концентраций в веществе метеороида.
Подобрав другие минералы с меняющимся содержанием в них того или иного элемента, мы получили бы несколько таких калибровочных кривых и смогли бы более надежно определять химический состав кометных метеороидов по спектрам метеоров, чем это делалось до сих пор. Применение этого метода в недалеком будущем позволит получить богатый материал о химическом составе малых тел Солнечной системы.
В заключение этого раздела расскажем о некоторых необычных эмиссиях в метеорных спектрах.
Одной из таких эмиссий является «запрещенная» зеленая линия атомарного кислорода с длиной волны 5577 А. Эта линия одна из главных в спектрах полярных сияний, но она наблюдается иногда и в спектрах метеоров.
Рис. 15. Соотношение концентраций натрия, магния и железа в углистых хондритах (СIII—СII—CI) и в метеорных телах, определенное по спектрам Драконид (D), Персеид (Р) и спорадических метеоров (N)
Рис. 16. Схема уровней и электронных переходов в атоме кислорода
Почему эта линия называется «запрещенной»? Она образуется в результате перехода с атомарного уровня 1S0, называемого метастабилъным, потому что при отсутствии внешних воздействий (например, ударов атомов или иных частиц) электрон удерживается на этом уровне очень долго — в среднем 0,75 с. В плотном газе этот уровень так долго «продержаться» не может — частые удары других атомов и свободных электронов вынуждают находящийся на уровне 1S0 электрон перейти на более высокие уровни. Атом не успевает испустить зеленую линию, соответствующую переходу 1S0 --> Спрашивается, почему же зеленая линия кислорода наблюдается в спектрах метеоров, а красный дублет нет. Здесь все дело в различии времен жизни. На высотах, где наблюдается зеленая линия (от 75 до 120 км), плотность воздуха (и газа в метеорной коме) достаточно мала, так что атом не успевает испытать столкновения с другими атомами в течение долей секунды, но она слишком велика, чтобы уберечь его от них в течение почти двух минут. Полярные сияния же наблюдаются и на гораздо больших высотах.
Но каким образом возбуждается метастабильный уровень 1S0 (рис. 16). Прямым возбуждением с основного уровня 3Р? Но такой переход запрещен правилами отбора Паули. За счет переходов с верхних уровней? А как могут возбуждаться они? Ведь для этого нужна большая энергия — 14,4 эВ, причем необходимые уровни лежат над порогом ионизации атома кислорода, иначе говоря, более вероятна ионизация атома, чем возбуждение уровня 1P10, с которого «разрешен» переход на исходный уровень 1S0, ответственный за испускание зеленой линии.
В 1960 г. канадский астроном Я. Холлидей (который и открыл двумя годами раньше зеленую линию в спектрах метеоров) предложил механизм возбуждения уровня 1S0 в метеорных следах за счет диссоциативной рекомбинации кислорода. Ион кислорода, сталкиваясь с молекулой, передает ей свой заряд, но зато, став нейтральным, возбуждается до уровня 1S0. Молекулярный ион, рекомбинируя со свободным электроном, диссоциирует на два атома кислорода, из коих первый возбуждается до состояния 1S0, а другой — до состояния 1D. Схема этого процесса выглядит так:
О+ + О2 --> О2+ + е --> Спустя 16 лет новозеландский астроном У. Баггали предложил еще один механизм — передачу энергии атому кислорода от возбужденных молекул азота. Сделать выбор между двумя этими механизмами затруднительно. Возможно, что проявляются они оба.
Поведение зеленой линии в метеорных спектрах имеет некоторые особенности. Она видна в перерывах, создаваемых обтюратором, и имеет продолжительность свечения до 1 с, а это значит, что свечение атомов кислорода происходит в ионном следе метеора. В годы максимума солнечной активности она наблюдается чаще и ее свечение прослеживается на более низких высотах, чем в годы минимума. Диапазон высот ее высвечивания соответствует области наибольшей концентрации атомарного кислорода в атмосфере Земли (максимум на 105 км). Это значит, что за формирование этой линии ответствен атмосферный кислород, а пролет метеора лишь возбуждает свечение. Зеленая линия наблюдается не только у ярких, но и у относительно слабых метеоров. Так, астрономы лаборатории физики метеорных явлений Физико-технического института Академии наук Туркменской ССР не раз регистрировали ее телевизионным способом у метеоров до 4-й звездной величины. Еще ряд особенностей поведения зеленой линии кислорода связан с другим явлением — головным эхо метеоров, о котором будет рассказано в следующем разделе.
На тех же спектрах слабых метеоров, полученных ашхабадскими астрономами с помощью телевизионной техники, были обнаружены полосы молекулярного иона азота N2+, принадлежащие к так называемой первой отрицательной системе полос, на длинах волн 4278 и 3914 А. В спектрах ярких метеоров эти полосы никогда не наблюдались. Автор этой книги нашел объяснение этому факту в следующем.
При полете ярких метеоров и болидов, когда имеет место сильная ионизация, молекулярные ионы азота образоваться не могут, поскольку они быстро рекомбинируют со свободными электронами и диссоциируют на два атома азота. Такую же роль могут играть и ионы металлов. При полете же слабых метеоров ионизация относительно слаба, свободных электронов в метеорном следе мало, а ионы металлов не успевают уничтожать молекулярные ионы азота, и они могут высвечивать в полосах первой отрицательной системы. Разумеется, все эти соображения явились лишь результатом соответствующих математических расчетов, в которых учитывалось более 20 химических реакций, приводящих к образованию и разрушению ионов N2+.
Метеорная ионизация
Пролетая с большой скоростью в верхних слоях атмосферы, метеороид испаряется, а испарившиеся атомы, сталкиваясь с набегающими атомами и молекулами воздуха, ионизируются и ионизируют атомы газов воздуха. На пути метеороида образуется ионно-электронный след, имеющий форму цилиндрической трубки, которая постепенно расширяется. В середине 40-х годов почти одновременно в СССР и в Англии были применены радиолокационные методы исследования метеоров. Выяснилось, что метеорные следы обладают способностью отражать метровые и декаметровые радиоволны. Появился новый мощный метод исследования метеоров, который начал быстро развиваться. Это вызвало необходимость построения теории метеорной ионизации, основы которой были заложены в 1948 г. норвежским исследователем Н. Херлофсоном. В дальнейшем большой вклад в теорию метеорной ионизации внесли советские ученые Ю. А. Лощилов, Е. И. Фиалко, К. В. Костылев, Б. Л. Кащеев и другие. Намного усовершенствовалась и техника радиолокации.
Ионно-электронные следы метеоров бывают разного типа. Если линейная электронная плотность (число электронов на 1 см длины следа) меньше 1012 эл./см, то каждый электрон отражает падающую на него радиоволну как бы сам по себе (рис. 17, а). Такой след называется ненасыщенным или недоуплотненным. Он как бы прозрачен для радиоволн. Если же линейная электронная плотность превосходит указанное выше значение, то вблизи оси следа образуется все увеличивающаяся в диаметре колонна, отражающая радиоволну как единое целое, как сплошная металлическая поверхность того же диаметра (рис. 17, б). Такие следы называют насыщенными или переуплотненными. Между этими типами метеорных следов различают еще следы переходного типа, у которых внутренняя часть отражает как насыщенный след, а внешняя — как ненасыщенный.
Рис. 17. Отражение радиоволн от ненасыщенного (а) и насыщенного (б) ионно-электронного следа
Точки — электроны; сплошные и штриховые прямые — соответственно падающие и отраженные радиоволны. Показаны только радиоволны, которые идут обратно к антенне
Линейная электронная плотность Однако определить вид этой зависимости было нелегко. Коэффициент ионизации зависит от отношения эффективных сечений двух процессов: ионизации и передачи импульса. Поскольку эффективное сечение — это величина, определяющая вероятность данного процесса (свое название она получила потому, что имеет размерность площади), сказанное выше равносильно утверждению, что коэффициент ионизации зависит от отношения вероятностей ионизации (неупругого процесса) и передачи импульса (упругого процесса).
В самом деле, из всех столкновений метеорных атомов с набегающими атмосферными подавляющее большинство — упругие, приводящие к торможению частиц метеорных паров относительно воздуха от метеорных до тепловых скоростей, с передачей импульса и энергии атомам атмосферы. По оценке Э. Эпика, только 3% всех столкновений неупругие, вызывающие возбуждение и ионизацию атомов. Но так как каждый метеорный атом испытывает не одно, а много столкновений, коэффициент ионизации может при известных условиях превышать единицу.
Зависимость коэффициента ионизации от скорости метеора имеет вид но в отношении значений Начальным периодом в образовании метеорного следа является его расширение до так называемого начального радиуса, когда еще не установилось тепловое равновесие с окружающей средой. Вопрос о начальном радиусе имеет большое значение в понимании физики метеорного следа и отражения им радиоволн. Поясним это подробнее.
Атомы, испаряющиеся с поверхности метеороида, имеют примерно такие же скорости, как и сам метеороид. Поэтому на первом этапе происходит быстрое расширение метеорного следа. Но дальше этот процесс резко замедляется, поскольку скорости движения атомов быстро приближаются к тепловым.
Приближенно начальный радиус метеорного следа выражается формулой
r0=2.6 1010v00.8/N,
где v0— начальная скорость метеороида, N — число атмосферных молекул в единице объема. Наблюдения подтверждают эту формулу, выведенную теоретически. В частности, метеор, имеющий скорость 40 км/с, создает на высоте 95 км след с начальным радиусом 1 м.
Тот факт, что начальный радиус следа порядка метра, подтверждается наблюдениями на различных длинах волн. Число наблюдаемых метеоров резко убывает с уменьшением длины волны ниже 6 м, т. е. с приближением отношения Интересная картина наблюдается при приеме отраженного радиосигнала от метеора (рис. 18). Сначала интенсивность плавно нарастает, поскольку в отражение радиоволн включаются все новые и новые участки следа. Но после того как метеор достигает так называемой зеркальной точки (точки траектории, в которой луч радиолокатора образует с ней прямой угол), интенсивность сигнала начинает колебаться около некоторого значения, то возрастая, то убывая. Это явление связано с дифракцией радиоволн и подобно зонам Френеля на краю изображения светящегося объекта. Причина его заключается в том, что сигналы, отраженные от части траектории, где метеор удаляется, приходят в разных фазах и то усиливают общий сигнал, то ослабляют его. Это зависит от того, в какой фазе приходит сигнал от нового участка траектории: в той же, что от зеркальной точки, или в противоположной.
Рис. 18. Записи дифракционной картины при радиоотражении от метеора (по Д. Мак-Кинли)
Дифракционная картина, регистрируемая на фотопленке (см. рис. 18), позволяет определить скорость метеора, поскольку на ней показано и изменение амплитуды сигнала в функции времени (амплитудно-временная характеристика). Если видно, что амплитуда сигнала испытывает не только периодические колебания, но и общее затухание (а чаще всего так и бывает), это означает, что след постепенно диффундирует в окружающий воздух и можно найти скорость диффузии. После того как след сформировался, начинается вторая фаза его существования — распад. Основным процессом, приводящим к распаду следа, является диффузия, в ходе которой след расширяется, плотность его падает и он перестает отражать радиоволны. Чем меньше был метеороид или чем меньшей скоростью он обладал, тем меньше будет начальная линейная электронная плотность следа, а значит, тем быстрее он разрушится.
Попробуем исключить влияние скорости метеора. Для этого будем выбирать метеоры какого-нибудь одного метеорного потока, у которых скорость одинакова. Построим для них диаграмму, изображающую распределение метеорных следов по длительностям. Получим картину, изображенную на рис. 19. Четко виден излом на кривой около длительности следа 10 с. Левая часть кривой (до излома) отражает действие диффузии на разрушение следа: по ее наклону можно определить распределение метеорных тел данного потока по массам.
Рис. 19. Распределение метеорных следов по длительностям отражения (по О. И. Бельковичу)
1— наблюдения в Душанбе, 2— в Казани
В чем же причина излома па этой кривой? Может быть, на кривой распределения метеорных тел по массам также имеется излом? Нет, другие способы исследования не подтверждают этого. Значит, при больших длительностях существования следа начинают проявляться, кроме диффузии, другие механизмы разрушения следа. Кропотливое исследование этого вопроса О. И. Бельковичем и его сотрудниками на Астрономической обсерватории им. В. П. Энгельгардта при Казанском университете, а также другими астрономами показало, что в интервале длительностей 10—50 с основную роль в ускорении разрушения следа играет прилипание электронов к молекулам кислорода с образованием отрицательных молекулярных ионов О2-. При длительностях, превышающих 50 с, начинает сказываться еще один механизм: турбулентная диффузия. Дело в том, что если диаметр следа в ходе его расширения превзойдет некоторую величину, называемую масштабом турбулентности, в следе будут образовываться турбулентные вихри и диффузия пойдет гораздо быстрее, чем при простом разбегании молекул. Вихреобразное движение частиц следа приведет к его быстрому разрушению. Последний механизм, влияющий на разрушение следа, — рекомбинация положительных ионов с электронами — играет по сравнению с другими механизмами подчиненную роль.
Рис. 20. Радиоотражение метеора на экране радиолокатора
По горизонтали — время; по вертикали — наклонная дальность. Полоска, идущая наискось слева, - головное эхо; широкая горизонтальная полоса - основное эхо
На экране радиолокатора основной след метеора, о котором мы до сих пор говорили, выглядит более или менее длинной горизонтальной полосой (рис. 20). Протяженность этой полосы в вертикальном направлении (ширина полосы) определяется интервалом высот, поскольку отражение от верхней части следа приходит позже, чем от нижней. (Собственно говоря, по вертикали на экране радиолокатора откладывается не высота, а наклонная дальность (расстояние до точки следа по прямой), но так как угол наклона луча известен, отсюда легко найти высоту). Протяженность полосы по горизонтали (в длину) определяется длительностью отражения, т. е. существования следа. Говоря короче, на экране радиолокатора реализуется развертка высота—время или наклонная дальность—время (от дальности нетрудно перейти к высоте).
А теперь обратим внимание на наклонную полоску слева на рис. 20. Это тоже радиоэхо, связанное с метеором. Поскольку оно расположено слева, очевидно, что это эхо формируется раньше основного отражения. Далее, хорошо заметно, что между этим головным эхо и основным отражением нет плавного перехода; это значит, что оба эхо имеют разную природу. Природу основного эха мы знаем — это отражение радиоволн ионно-электронным следом метеора. А какова природа головного эха?
Тот факт, что полоска головного эха на экране расположена наклонно, показывает, что источник отражения радиоволн движется вместе с метеором. Длительность головного эха, как показали исследования чехословацких и канадских астрономов, меньше 0,002 с. Интервал высот, на которых наблюдается головное эхо, по П. Миллману, равен 87—118 км.
Прежде чем ответить на вопрос о природе головного эха, обратим внимание на связь этого явления с образованием в спектрах метеоров зеленой запрещенной линии кислорода 5577 А. Для этого перечислим некоторые факты, относящиеся к обоим явлениям.
1. Как головное эхо, так и зеленая линия наблюдаются не только у ярких метеоров, но и у метеоров средней яркости — до 2-й звездной величины. Интервалы высот для обоих явлений почти одинаковы, но головное эхо начинается выше, чем основное (это видно и на рис. 20).
2. И головные эхо, и зеленая линия чаще встречаются у быстрых метеоров.
3. Оба явления сохраняют более или менее постоянную интенсивность вдоль пути метеора.
4. Протекание обоих явлений зависит от условий в атмосфере в интервале высот 87—118 км.
5. Наблюдается зависимость частоты появления и высот свечения зеленой линии от солнечной активности. Для головных эхо эта связь выражена менее отчетливо и вопрос не может считаться выясненным.
Теперь во всеоружии накопленных наблюдательных фактов попробуем дать объяснение явлению головного эха. В этом мы будем следовать исследованию чехословацкого астронома Я. Райхля.
Итак, ясно, что источник головного эха движется вместе с метеором. Это своеобразный «сгусток ионизации», как назвали его канадские астрономы П. Миллман и Д. Мак-Кинли, одни из первых обнаружившие это явление. Но за счет чего образуется этот сгусток? Миллман и Мак-Кинли полагали, что причиной его образования является мощное ультрафиолетовое излучение ударной волны, создаваемой метеороидами. Но ударную волну может образовать только достаточно крупное тело (на тех высотах, где наблюдаются головные эхо, необходимы тела больше метра). А как же быть с головным эхо у сравнительно слабых метеоров?
Я. Райхль объяснил это явление тем, что при определенных условиях (каких именно, мы объясним ниже) перед метеороидом образуется так называемый слой взаимодействия, в котором происходит взаимодействие отраженных, испаряющихся и набегающих молекул, развиваются такие процессы, как возбуждение, ионизация и диффузия.
Однако диффузия — слишком медленно действующий механизм, чтобы объяснить краткость головного эха. Здесь требуется рекомбинация, но ее скорость должна быть раз в 20—50 больше, чем в обычных (равновесных) условиях. Я. Райхлю удалось, опираясь на экспериментальные результаты и теорию начальной стадии неравновесной диссоциативной рекомбинации, показать, что на этой стадии скорость реакций, приведенных на с. 65, действительно может превышать свое равновесное значение на один-два порядка. А ведь эти реакции с диссоциативной рекомбинацией кислорода объясняют, как мы уже знаем, возбуждение уровня 1S0 в атомах кислорода, переход с которого приводит к излучению зеленой линии 5577 А.
Так Я. Райхлю удалось с единой точки зрения объяснить два, казалось бы, совершенно различных явления — головное эхо и свечение запрещенной зеленой линии кислорода. Оставалось выяснить, при каких условиях формируется слой взаимодействия, в котором и происходит диссоциативная рекомбинация, обеспечивающая оба явления. Райхль подсчитал, что для существования этого слоя необходимо, чтобы отношение диаметра тела 2R к длине свободного пробега молекул I, исправленное за отношение скоростей набегающих и отраженных молекул (соответственно, v, vr), то есть число
заключалось в пределах от 0,1 до 10. Для тел диаметром 1 см это условие реализуется в интервале высот 80—115 км, а для тел диаметром 10 см — в интервале 87-118 км.
Но это же и есть тот интервал высот, на котором наблюдаются зеленая линия и головное эхо! И выбор размеров тел здесь не случаен. У меньших тел слой взаимодействия не образуется, а у больших тел формирование ударной волны впереди тела прерывает действие механизма Райхля — ионизацию набегающих атомов кислорода отраженными и испаряющимися молекулами. Зато после сформирования ударной волны возможна их ионизация опережающим излучением (которое предполагали П. Миллман и Д. Мак-Кинли) или на фронте самой ударной волны в процессах столкновений. О том, как развиваются эти процессы, мы расскажем ниже.
Радиолокационные наблюдения метеоров позволяют определять не только характеристики самого метеора и его следа. По смещению (дрейфу) метеорных следов можно составить представление об особенностях циркуляции атмосферы в метеорной зоне (в интервале высот, где наблюдаются метеоры), причем на разных широтах в разное время года и суток, выявлять закономерности циркуляции верхней атмосферы. Но мы здесь эти вопросы рассматривать не будем.
Метеороиды и ударные волны
Мы уже не раз говорили о том, что крупные метеороиды образуют ударные волны. Познакомимся с этим явлением поближе.
При движении любого достаточно крупного тела со сверхзвуковой скоростью в плотном газе, который можно рассматривать как сплошную среду, впереди тела образуется скачок уплотнения газа, именуемый ударной волной. На фронте ударной волны скачком возрастают давление, плотность и температура набегающего газа, а скорость движения молекул относительно тела падает. Причина этого явления состоит в том, что при сверхзвуковом движении тела встречные молекулы не успевают перед ним расступаться или передавать свою энергию и импульс другим молекулам. Перед телом образуется уплотненный, или, как чаще говорят, сжатый слой молекул (он называется также ударным слоем) (рис. 21). Впервые ученые встретились с явлением ударных волн при попытках летчиков преодолеть так называемый звуковой барьер, т. е. летать на самолетах быстрее звука. Скорость звука в воздухе при нормальных условиях равна 330 м/с (1200 км/ч) и изменяется пропорционально его абсолютной температуре. Попытки летчиков преодолеть звуковой барьер (а мощность двигателей давала им такую возможность) заканчивались сперва трагически: самолеты разваливались, пилоты погибали или спасались на парашютах. Так продолжалось до тех пор, пока ученые не объяснили, что причиной этих аварий была ударная волна от носовой части фюзеляжа, которая в буквальном смысле обрубала самолетам крылья, располагавшиеся по прямой линии перпендикулярно фюзеляжу. Лишь после того как конструкторы, учтя соображения ученых, стали строить самолеты с крыльями, скошенными назад, аварии прекратились и звуковой барьер был взят.
Рис. 21. Основные элементы ударной волны: 1 — ударный фронт; 2 — сжатый слой; 3 — пограничный слой; 4 — застойная зона; 5 — турбулентный след
Отношение скорости тела к скорости звука в данной среде называется числом Маха. Для метеоров, влетающих в нашу атмосферу со скоростями от 11 до 72 км/с, число Маха оказывается в пределах от 33 до 216 (очень большое число Маха). Движение с такими скоростями называют даже не сверхзвуковым, а гиперзвуковым. На фронте ударной волны давление скачком возрастает во много раз. Отношение давлений за скачком и перед ним приближенно равно квадрату числа Маха. Для приведенных выше чисел Маха это отношение может заключаться между 1000 и 46 500. Но плотность газа за фронтом не может возрасти более чем в 10—12 раз (и то только в случае очень сильных ударных волн). Это означает, что в сжатом слое должна сильно повыситься температура. Если давление увеличится, например, в 10 000 раз, а плотность — в 10 раз, то по законам состояния газа его температура должна возрасти в 1000 раз.
В действительности, однако, так не происходит. При разогревании газа значительная часть энергии уходит на возбуждение внутренних степеней свободы молекул газа: на возбуждение колебаний атомов в молекулах, на их диссоциацию, на возбуждение и ионизацию атомов. Поэтому хотя температура сжатого слоя и возрастает, но лишь до тысяч и десятков тысяч градусов, а не до сотен тысяч, как следовало бы на основании чисел, приведенных выше.
Так или иначе, по газ за фронтом ударной волны перед летящим метеороидом приобретает свойства плазмы, в которой может происходить не только однократная, но и многократная ионизация атомов. Правда, линий даже двукратных ионов в спектрах ярких болидов пока не обнаружено, но это связано с тем, что линии таких ионов расположены в ультрафиолетовой части спектра, для нас (с поверхности Земли) практически не наблюдаемой. Причиной этого является слой озона, расположенный на высотах 20—50 км в нашей атмосфере и поглощающий все ультрафиолетовые лучи с длиной волны короче 3500 А. (Тем самым он защищает все живое от губительной ультрафиолетовой радиации Солнца и других космических объектов.)
Ударный слой является источником мощного излучения. Это излучение формируется двумя путями. Во-первых, возбужденные атомы за счет переходов электрона с верхних уровней на нижние излучают в спектральных линиях. Во-вторых, при рекомбинации свободных электронов с ионами генерируется излучение в непрерывном спектре (в основном в ультрафиолетовой области). Часть этого излучения после поглощения в самом ударном слое и в слое метеорных паров попадает на поверхность тела, производя его плавление и испарение. Другая часть излучения высвечивается наружу. Поскольку самые горячие области плазмы сжатого слоя расположены перед носовой точкой тела (ее называют критической точкой), наиболее мощное излучение направлено прямо вперед по его движению. Оно прогревает и ионизирует газ впереди ударной волны, что может в случае ярких болидов привести к образованию того «сгустка ионизации», о котором писали Миллман и Мак-Кинли, пытаясь объяснить головные эхо метеоров.
Форма ударной волны зависит от формы тела. Перед тупыми телами образуется отсоединенная ударная волна, нигде не соприкасающаяся с самим телом. Ее расстояние от поверхности тела в районе критической точки составляет примерно 15% радиуса кривизны тела в этой точке. Дальше ударная волна постепенно отходит от тела. На больших расстояниях она имеет форму очень узкого конуса с малым углом раствора.
Если тело имеет острый выступ впереди или само подобно конусу, то ударная волна начинается прямо от острия и называется присоединенной. В действительности метеорные тела имеют неправильную форму, и поэтому перед ними образуется сложная система ударных волн (см. вкл.).
Ударные волны и акустические явления
После пролета крупного метеороида образованная им ударная волна начинает расширяться, расходиться во все стороны, в том числе и к земной поверхности. При этом волна, идущая вниз, постепенно замедляет свое движение и теряет энергию. Это происходит по двум причинам. Во-первых, по мере распространения волны в движение вовлекаются все новые и новые объемы воздуха, а на их разгон требуется энергия. Кроме того, за фронтом волны воздух, как мы знаем, нагревается, на что тоже расходуется энергия. Этот фактор действует независимо от направления распространения волны. Во-вторых, при распространении вниз ударная волна встречает все более плотные слои воздуха, в движение приходится вовлекать (в том же объеме), все большее число молекул, поэтому ударная волна, идущая вниз, теряет энергию и скорость сильнее, чем волна, идущая вверх. Более того, при известных условиях ударная волна, идущая вверх, может начать ускоряться (за счет падения давления с высотой и перетекания энергии внутри волны снизу вверх).
Но сейчас нас интересуют именно ударные волны, распространяющиеся от летящего метеороида вниз, к земной поверхности. Достигнув ее, они производят звуковые явления, которые воспринимаются очевидцами как гром, грохот, пальба из орудий. После пролета знаменитого Тунгусского метеорита 1908 г. многие сибирские крестьяне, услышав такие звуки, решили даже, что возобновилась война с Японией.
Хотя в первые секунды после пролета метеороида скорость распространения ударной волны в несколько раз превосходит скорость звука, она довольно быстро падает до значений, лишь не намного больших звуковой скорости, поэтому в приближенных расчетах можно использовать скорость звука в воздухе — 330 м/с. А это значит, что с расстояния 100 км (типичное расстояние от наблюдателя до болида) звуковая волна дойдет за 300 с (или за 5 мин).
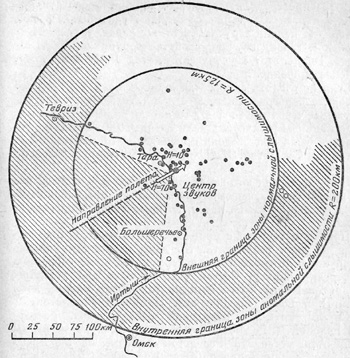
Область слышимости акустических явлений от крупных болидов и падающих на Землю метеоритов делится на три зоны. Первая зона, прилегающая к месту падения метеорита или к траектории болида, называется зоной нормальной слышимости звуков. Далее идет зона, где звуки из-за дальности уже не слышны. И, наконец, еще дальше звуки снова становятся слышны из-за отражения звуковых волн от верхних слоев атмосферы. Это зона аномальной слышимости звуков (рис. 22).
Рис. 22. Звуковые явления при падении метеорита Хмелевка 1 марта 1929 г.
В заштрихованной области звуки слышны не были. Точки — места расположения наблюдателей
По распространению звуковых волн от пролета и падения метеоритов, а также от мощных наземных взрывов раньше (до начала запуска высотных ракет, т. е. до середины 40-х годов) изучали свойства верхних слоев атмосферы. Теперь этот акустический метод имеет лишь историческое значение.
Если не считать записей воздушных волн Тунгусского метеорита барографами ряда стран (эти записи были обнаружены через много лет), то первая инструментальная регистрация акустических волн летящего в атмосфере метеороида была произведена при падении 31 марта 1965 г. метеорита Ревелсток. История этого метеорита довольно необычна.
В эту ночь над юго-западной Канадой наблюдался полет яркого болида, рассыпавшего искры и раздробившегося на высоте 30 км на части, которые исчезли на высоте 12 км.
Поиски метеорита с привлечением самолетов и вертолетов не дали результата. Но двум охотникам удалось обнаружить на свежем снегу черную пыль. Ее собрали и подвергли анализу. Состав был типичен для углистых хондритов I типа. Эти крупинки (их общая масса — доли грамма) и носят звучное имя «метеорит Ревелсток».
Спустя пять лет канадский исследователь метеорных явлений Д. Ре Велле установил, что звуковые волны от пролета метеорита Ревелсток записаны на барограмме метеостанции Боулдер (штат Колорадо, США). Вскоре на барограммах той же станции были обнаружены записи звуковых волн еще от двух ярких болидов. Запись одного из них, пролетевшего 14 декабря 1968 г. над штатом Аризона, была найдена также на метеостанции во Флагстаффе, находившейся всего лишь в 150 км от траектории. Запись звуковых волн четвертого болида, наблюдавшегося 19 декабря 1969 г. над Аляской, была обнаружена на метеостанции Колледж (Аляска). Расстояния от станции наблюдения до траектории болида находились в пределах от 150 до 2500 км.
Обработка записей показала, что звуковые колебания имели некоторую периодичность: от 3—4 до 54 с у разных болидов. Длительность звуковых явлений составила от 10—12 с (болид Холбрук, Аризона) до 34 мин (болид Кинкардин, Онтарио). Звуковые явления от полета метеорита Ревелсток продолжались 20 мин.
Ре Велле сумел по амплитудам звуковых колебаний рассчитать начальную кинетическую энергию метеороидов: от 1018—1019 эрг для Холбрука (по наблюдениям с двух станций) до 3 1022 эрг для Кинкардина. Получалось, что начальная масса второго метеороида составляла 60 000 т! Есть, однако, веские основания полагать, что эта оценка сильно завышена.
Совсем иным путем были записаны звуковые волны от метеорита Боведи—Спрюсфилд, упавшего 25 апреля 1969 г. в Северной Ирландии. Полет болида наблюдался тысячами очевидцев на Британских островах вплоть до Лондона. Он летел с юго-востока на запад—северо-запад, а метеориты упали недалеко от Белфаста, в поселках Боведи (кусок 5 кг) и Спрюсфилд (два осколка массой 280 и 230 г), на расстоянии 50 км друг от друга.
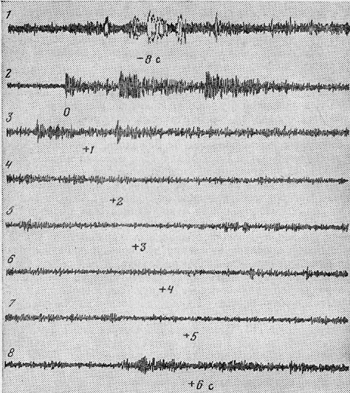
В эту же ночь некая мисс Э. Браун, проживавшая в городе Багнор, тоже недалеко от Белфаста, решила записать на магнитофон пение птиц. Запись шла нормально, как вдруг появился болид. Он привлек внимание не только людей, но и собак, поднявших отчаянный лай. Когда мисс Браун прослушала пленку, то снова услышала и пение птиц, и раскатистый гул от болида, и лай собак. Она поняла, что запись может представить интерес для науки и передала ее профессору Э. Эпику. Тот, в свою очередь, переслал копию записи, в Канаду известному исследователю метеоров П. Миллиону. С записи была сделана осциллограмма (рис. 23). Оказалось, что частота шума от болида — от 200 до 400 Гц, что соответствует музыкальным частотам от нижнего соль до соль малой октавы. Длительность отдельных звуковых импульсов — от 0,01 до 0,11 с, а общая продолжительность звуков — 5,5 с, но может быть, и дольше, поскольку потом слабеющий гул болида потонул в собачьем лае.
Рис. 23. Магнитофонная запись звуков при полете метеорита Боведи-Спрюсфилд 25 апреля 1969 г.
Колебания с большой амплитудой на строках 1—3 — звуки от болида; на строке 8 — лай собак
Эта уникальная запись прошла столь успешно не только благодаря случайному стечению обстоятельств (ведь мисс Браун, налаживая все для записи пения птиц, и представить себе не могла, что пролетит болид), но и потому, что Багнор, где жила мисс Браун, находился лишь в 45 км от траектории болида.
Впрочем, такие благоприятные стечения обстоятельств случались и раньше. Когда художник П. И. Медведев садился морозным утром 12 февраля 1947 г. за мольберт, чтобы написать наш дальневосточный пейзаж, он и не предполагал, что перед его глазами пронесется знаменитый Сихотэ-Алинский метеорит, оставляя за собой дымный след, и что именно это зрелище будет им увековечено на картине, которая станет научным документом и будет приобретена Комитетом по метеоритам АН СССР (см. фото.).
В конце 1974 г. канадские астрономы сконструировали и запустили в действие специальную установку для регистрации инфразвуковых волн от ярких метеоров и болидов на частотах около 1 Гц (в пределах от 0,2 до 5 Гц). Установка состояла из четырех микрофонных датчиков, расположенных в вершинах четырехугольника на расстояниях 135—240 км друг от друга, электронного и записывающего устройств.
Уже 14 декабря 1974 г. канадцам удалось записать инфразвуковые колебания от яркого метеора, зафиксированного также радаром. Амплитуда воздушных волн достигла 8 мкбар, их длительность — 7 с.
22 апреля 1975 г. на двух микробарографах станции Боулдер (штат Колорадо, США) были зарегистрированы воздушные волны от болида -5-й звездной величины, имевшие амплитуду 1 мкбар и период 1 с.
Таким образом, инструментальная регистрация воздушных волн, возникающих от пролета метеороидов в атмосфере, стала проводиться систематически. Канадский астроном Д. Ре Велле попытался построить теорию, которая позволяла бы по этим регистрациям определять параметры самих метеорных тел и условий их движения. Но для проверки этой теории наблюдательных данных еще недостаточно.
Электрофонные болиды
Среди разнообразных явлений, сопровождающих влет в атмосферу очень ярких болидов, особое место занимают звуковые явления, слышимые одновременно с полетом болида. Они не имеют ничего общего с обычными звуковыми волнами, распространяющимися со скоростью звука и достигающими наблюдателя спустя десятки секунд или минуты после пролета болида. По сообщениям многочисленных наблюдателей, при пролете очень ярких болидов бывают слышны свистящие или шуршащие звуки, причем нередко кажется, что они исходят не от болида, а от окружающих предметов. По предложению П. Л. Драверта, такие болиды получили название электрофонных. На существование аномальных звуков при полете ярких болидов впервые обратил внимание Э. Ф. Хладни еще в 1794 г. Впоследствии большинство специалистов отрицало факт электрофонных явлений на том основании, что скорость звука много меньше скорости света и потому звуковые явления от полета болида не могут восприниматься наблюдателем одновременно с самим болидом. Многочисленные сообщения наблюдателей электрофониых явлений эти специалисты истолковывали как результат психологического воздействия полета яркого тела, которое ассоциируется с полетом ракет, снарядов и т. п., когда звук не намного отстает но времени от полета самого тела. По мнению этих лиц, наблюдателю кажется, что он слышит звуки, которых в действительности нет. Поэтому такие исследователи, как Д. Кирквуд в своей «Метеорной астрономии» (1867), О. Фаррингтон в книге «Метеориты» (1915) и Ч. Оливье в книге «Метеоры» (1925), даже не упоминают об электрофонных болидах, хотя наблюдения этих явлений несомненно им были известны. Другие исследователи, как, например, К. Уайли, не замалчивая факты наблюдений аномальных звуковых явлений при пролете ярких болидов, дают им чисто «психофизиологическую» интерпретацию. В нашей стране такой точки зрения долго придерживался Б. Ю. Левин.
Как будет показано в дальнейшем, «психофизиологическая» интерпретация электрофонных болидов не имеет под собой никаких оснований и противоречит сотням наблюдений, часть из которых выполнена астрономами-специалистами или при таких условиях, которые полностью исключают воздействие зрелища летящего болида на психику наблюдателя (наблюдения в закрытых помещениях или лицами, не видевшими болид, или заметившими его после того, как они услышали звуки).
Первое систематическое исследование электрофонных болидов принадлежит И. С. Астаповичу. В 1925 г. семнадцатилетним юношей он наблюдал яркий электрофонный болид, произведший на него глубочайшее впечатление. Это побудило его изучить литературу, где он нашел множество других наблюдений аналогичных явлений. В 1929 г. И. С. Астапович составил первый каталог электрофонных болидов, включающий около 40 наблюдений. В 1951 г. был опубликован составленный им более подробный каталог 163 электрофонных болидов, включавший данные первого каталога, а также сообщения древних летописей и хроник начиная с 585 г. Спустя три года на страницах сборника «Метеоритика» было помещено дополнение к этому каталогу, основанное на материалах Комитета по метеоритам АН СССР и содержащее наблюдения еще 63 электрофонпых болидов. Третий каталог, включающий наблюдения 41 электрофониого болида, был составлен американскими учеными М. Ромиг и Д. Ламаром. Таким образом, все три опубликованных каталога содержали 267 наблюдений, выполненных до 1962 г. Недавно автор данной книги, В. С. Гребенников и Д. Д. Рабунский составили четвертый каталог, включивший 350 наблюдений, выполненных как за последние 20— 30 лет, так и в более ранние годы, но пропущенных составителями трех первых каталогов. Так что общее число наблюдавшихся электрофонных болидов — около 600.
Большинство наблюдателей определяют характер звуков, слышимых одновременно с полетом болида, как свистящий или шипящий. Вот несколько описаний: «легкий свист, какой издает быстро несущееся тело» (Б. Л. Глазман, Лубны); «был слышен шум со свистом и шипением» (В. Ф. Иванов, Ставрополь); «было слышно шипение... сравнимое с шипением большой змеи» (П. Кашбулин, ст. Туркестан); «шипение огня, на который попадает вода» (астроном А. Л. Зельманов); «звук повышался вверх (у-у-у-у!), убыстряясь в высоте тона, быстро оборвался» (музыкант А. Н. Пейч, Ашхабадская обл.); «звук как бы песка, сыплющегося по листьям дерева» (профессор Я. А. Мохаммед Хан, Индия); «свист, подобный свисту выключаемого мотора в самолете» (наблюдатель в штате Техас, США). Приводимые сравнения дают ясное представление о характере звуков.
Приведем также ряд свидетельств, явно противоречащих «психофизиологической» гипотезе.
«Позади нас раздался звук вроде взлетающей ракеты — тшшш-и-йох! и земля осветилась на миг; быстро обернувшись, я и Г. Блохин увидели след исчезнувшего болида» (И. С. Астапович, 20 августа 1925 г.).
«Услышал сильный шум, вроде шума бури по тайге... Обернувшись через 1—2 с на шум, увидел светящееся тело, очень яркое» (С. С. Козозаев, с. Хасурта, близ Верхнеудинска, Иркутская обл., 27 мая 1927 г.).
«Вдруг раздался сильный взрыв, как треск проводов, ослепительный свет магния; мы решили, что это сгорел па столбах провод, но треск и затухание света продолжались, свет электрический горел; я тогда отбежала на середину улицы и увидела... падение метеорита» (Л. И. Романад, Ашхабад, лето 1937 г.).
«Появление было замечено но звуку, который предшествовал (болиду); посмотрев по направлению звука, увидел как бы приближавшийся светящийся предмет» (А. Л. Зельманов, в то время аспирант МГУ, с парохода на Каспийском море, 17 декабря 1941 г.).
Все приведенные выдержки заимствованы из каталога И. С. Астаповича. Аналогичные факты приводят М. Ромиг и Д. Ламар, хотя они не сообщают фамилии наблюдателей. Так, наблюдатель в Сан-Антонио (штат Техас, США) 23 июня 1928 г. услышал шипение и поднял голову, чтобы увидеть предмет, производящий шум. Это оказался болид. Очевидец болида 8 августа 1933 г. (падение метеорита Небраска) находился в доме, услышал шум, подобный звуку самолета, делающего крутой вираж; когда он подошел к двери, метеор стал виден с юго-востока. Два или три наблюдателя падения метеорита Арчи (штат Миссури, США) 10 августа 1932 г. утверждали, что их внимание к метеору было привлечено свистящими звуками и что только тогда они посмотрели вверх и увидели его полет. 18 февраля 1948 г. игравший в баскетбол мальчик услышал особенный свист или шипение; посмотрев вверх, он увидел огненный шар, движущийся на восток (падение метеорита Нортон Каунти, штат Канзас, США).
Таких примеров можно было бы привести еще немало. Мы приведем лишь еще одно наблюдение, сообщенное автору биологом В. С. Гребенниковым, проживавшим в г. Исилькуле Омской области. Дело было в 1958—1960 гг. поздним зимним вечером (точной даты наблюдатель не помнит). Вот как описывает событие В. С. Гребенников: «...в зените был услышан громкий звук, очень похожий на неровный треск распарываемой или разрываемой ткани, чуть с металлическим тембром. Машинально я быстро вздернул голову. В районе зенита с СЗ на ЮВ быстро летел яркий белый метеор...».
Все приведенные факты (и многие аналогичные им, собранные в упомянутых каталогах) ясно показывают, что они не могут быть объяснены с позиций «психофизиологической» гипотезы. Во многих случаях звуки не только предшествовали визуальному наблюдению болида, но и послужили причиной того, что наблюдатели обратили внимание на самый полет небесного тела.
Еще более показательны в этом отношении данные наблюдений яркого электрофонного болида 7 апреля 1978 г., пролетевшего над густо населенными районами Нового Южного Уэльса (Австралия), включая г. Сидней.
Этот болид — 16-й звездной величины (в 15 раз ярче полной Луны) наблюдался ранним утром над восточным побережьем Нового Южного Уэльса несколькими сотнями очевидцев. Примерно треть из них сообщила об аномальных звуках, синхронных с полетом болида. Все наблюдения аномальных звуков были собраны и обработаны астрономом К. Кэем. Ему удалось опросить 33 очевидца болида, из них 10 человек сообщили, что слышали аномальные звуки. Трое из этих десяти с определенностью заявили, что они сперва услышали звуки, а уж потом заметили сам болид. По оценке К. Кэя, выход энергии метеороида во время максимального блеска 4 1011 Вт. Мощность же излучения составила 109 Вт, т. е. доли процента от общей энергии тела.
Пролет столь яркого электрофонного болида побудил К. Кэя исследовать возможные физические причины слышимости звуков, одновременных с полетом болида, а также поставить некоторые эксперименты.
Поиски механизма аномальных звуков велись еще с 30-х годов. Все предлагавшиеся механизмы можно разделить на две группы.
1. Механизмы, предполагающие перенос энергии электромагнитными волнами на радиочастотах или еще более низких частотах с последующим выпрямлением их и преобразованием в звуковые волны в непосредственной близости от наблюдателя.
2. Электростатический механизм, т. о. возникновение наведенных зарядов на близлежащих предметах, а затем стекание заряда, сопровождающееся звуковыми явлениями.
Пожалуй, первая попытка теоретического анализа второго механизма была предпринята В. В. Ивановым и Ю. А. Медведевым в 1965 г. Они показали, что в некоторой области за фронтом ударной волны, окружающей метеороид, происходит вытеснение электрического поля из области ионизации, причем эта область приобретает дипольный момент, направленный против электрического поля Земли. Наводимые потенциалы могут составить несколько сотен вольт для крупных метеороидов при вертикальном движении. Однако электростатический механизм не согласуется с показаниями очевидцев, которые ясно указывают, что звуки исходят не от окрестных предметов, а сверху, от летящего болида (см. приведенные выше описания И. С. Астаповича, С. С. Козозаева, А. Л. Зельманова, В. С. Гребенникова).
Остается предположить, что возмущение передается от болида со световой скоростью, т. е. в виде радиоволн, которые уже внизу трансформируются в звук. В том, что это действительно возможно, нас убеждают эксперименты К. Кэя.
Кэй усаживал испытуемых в звукоизолированной комнате и подвергал их воздействию переменного электрического поля с амплитудой 130 В/м и звуковой частотой (несколько килогерц). И при этом испытуемые слышали звуки! Те, у кого были длинные волосы или очки в металлической оправе, слышали звуки лучше. Волосы и оправа очков тоже (наряду с ушной раковиной) становились детекторами электромагнитных колебаний и превращали их в звуковые волны.
Известный астроном, исследователь планет Л. В. Ксанфомалити рассказывал автору, что при приеме излучения мощного радиоисточника на параболическую антенну он ясно слышал сильное гудение.
Итак, радиоволны способны преобразовываться в звук. Но откуда берутся они сами? Что служит механизмом их генерации?
К. Кэй, перебрав несколько механизмов, остановился на следующем.
При вторжении в атмосферу Земли крупного метеороида, наблюдаемого в виде яркого болида, образуется, как мы знаем, ионно-электронный след, движущийся вместе с болидом и претерпевающий диффузное расширение. В случае ярких метеоров и болидов мы всегда имеем дело с насыщенными следами, практически непрозрачными для радиоволн не только килогерцевого, но и мегагерцевого диапазона.
В метеорном следе возникает турбуленция. Турбулентные вихри могут при известных условиях закручивать силовые линии магнитного поля Земли, и тогда напряженность поля в следе болида резко возрастает. Спустя некоторое время это поле разрушается, отдавая свою энергию окружающему пространству, в том числе и в виде радиоволн.
Идея Кэя была очень интересна, но не имела строгого теоретического обоснования. Получить его удалось автору этой книги.
Прежде всего было найдено условие, при котором данный механизм будет действовать. Для этого проводимость плазмы метеорного следа должна превышать некоторое критическое значение. Это обстоятельство объясняло давно уже установленный И. С. Астаповичем факт, что только очень яркие болиды (ярче -9-й звездной величины) порождают электрофонные явления.
Были вычислены характерные времена усиления и распада магнитного поля в следе. Они оказались достаточно малыми (10-3 и 10-2 с соответственно), так что участок следа с усиленным полем не превышал по длине нескольких сотен метров. При распаде поля большая часть его энергии переходит в джоулево тепло. Лишь около 0,1% превращается в радиоволны. Хватит ли этой энергии, чтобы создать ощутимый нашим ухом звуковой эффект на расстоянии около 100 км от болида?
Расчеты показали, что хватит. Даже с учетом того, что наше ухо — очень плохой выпрямитель, с низким КПД.
В самом деле, лучшие приемные устройства в радиоприемниках имеют КПД около 20%, большинство же — немногие проценты. Но даже КПД в 0,1% достаточен, чтобы слышать звук типа шороха или свиста.
К сожалению, мы не располагаем инструментальными записями аномальных звуков, как это имеет место с нормальными звуками, о которых писалось выше. Подстеречь электрофонный болид далеко не просто — это очень уж редкое явление. Правда, есть несколько свидетельств приема собственных радиоволн метеоров и болидов. Так, еще в конце 40-х годов И. С. Астапович в Ашхабаде провел ряд успешных попыток зарегистрировать собственное радиоизлучение метеоров. В то же годы радист одного из наших кораблей, плававших в Северном Ледовитом океане, Ю. Н. Хлюстов систематически отмечал совпадение по времени радиосигналов, слышимых в приемнике, и пролета ярких метеоров. С другой стороны, специальные наблюдения американского исследователя метеоров Дж. Хокинса не дали результата. Правда, Хокинс наблюдал метеоры не ярче нулевой звездной величины, тогда как метеоры, зафиксированные Хлюстовым, были в 6—40 раз ярче.
Попытки возобновить подобные наблюдения в 60-е годы натолкнулись на громадное количество радиопомех из-за развития сети радиостанций и частных передатчиков во всем мире.
Есть, однако, целый ряд объективных фактов электромагнитных воздействий ярких болидов на земные объекты. Во время полета Сихотэ-Алинского метеорита монтер А. В. Ефтеев, чинивший телефонные провода, ощутил удар тока, хотя линия была отключена. При пролете Чулымского болида 26 февраля 1984 г. в Западной Сибири в некоторых пунктах перегорели лампочки, наблюдались помехи на экранах телевизоров, вышли из строя фотоэлементы ламп дневного света. Все это свидетельствует о мощном электромагнитном поле, порожденном болидом. Исследование электромагнитных явлений, связанных с полетом метеоров и болидов в атмосфере, только начинается. Несомненно, оно принесет много интересного.R2, V=(4/3)
R3, A~1,21, для цилиндра, летящего торцом вперед (S=
R2, V=
R2l), A=1,46
v, умноженному на кинетическую энергию единицы массы v2/2, т. е. S
v3/2. Но из-за эффектов загораживания отлетающими и испаряющимися молекулами, описанных выше, до тела доходит не вся эта энергия, а лишь некоторая ее доля
. Величина
называется коэффициентом теплопередачи. Она может равняться единице на самом верхнем участке пути, где плотность атмосферы мала и загораживание незначительно, и уменьшается до десятых и даже сотых долей на нижнем участке траектории метеора из-за сильного загораживания в основном испаряющимися молекулами.
S
v3/2Q,
(dM/dt) (v2/2).
S
v5/4Q.
сам зависит от скорости.
=
0v
(v)
![]() , имеющего диаметр диска d
, имеющего диаметр диска d![]() = = 1800" и температуру Т
= = 1800" и температуру Т![]() =6000 К. Тогда
=6000 К. Тогда
![]() =2.5 lg [(d
=2.5 lg [(d![]() /dM)2 (Т
/dM)2 (Т![]() /ТM)4],
/ТM)4], ![]() — Солнцу. Произведя вычисления, найдем
— Солнцу. Произведя вычисления, найдем ![]() =31.0, m
=31.0, m![]() =-26.7
=-26.7 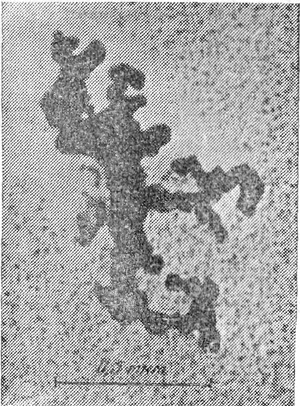
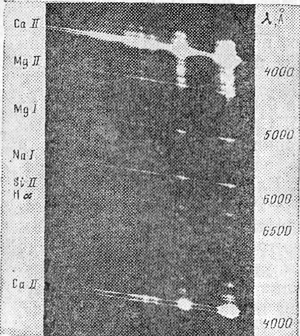
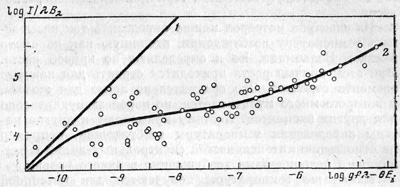

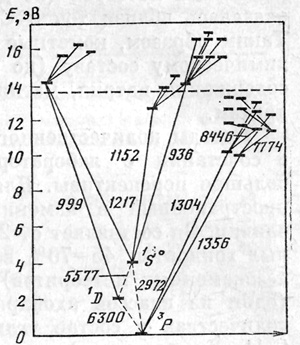
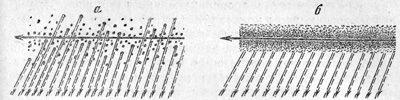
=
0vk,
0
0<쿀ȄꦜΆ춬瘡ࠀ˵節˵>