К ОПРЕДЕЛЕНИЮ ЭПИЦЕНТРА ВЗРЫВА ТУНГУССКОГО МЕТЕОРИТА ПО ХАРАКТЕРУ ВЫВАЛА ЛЕСА
В. Г ФАСТ
В районе взрыва Тунгусского метеорита наблюдается мощный радиальный вывал леса на площади около 2000 кв. км. Естественно попытаться по направлению повала деревьев определить эпицентр взрыва. Такая попытка впервые была предпринята Л. А. Куликом в 1938 г. [1, 2, 3] на основании полевой мозаичной аэрофотосхемы центральной площади вывала, незначительно выходившей за пределы котловины. Л. А. Куликом были получены четыре центра генерации ударных волн, из которых, однако, только западный центр на Южном болоте считался надежно установленным [3]. В настоящей статье предпринята попытка определения эпицентра взрыва на основании полевых измерений, проведенных экспедицией 1960 г. Основную роль при этом играли измерения, проведенные на более далеком расстоянии (4—22 км) от эпицентра.
Измерения азимутов поваленных деревьев проводились четырьмя радиальными группами, вышедшими от изб Кулика по азимутам 18°, 140°, 215°, 295°, и четырьмя лесотаксационными группами, вышедшими из общего центра, находящегося на расстоянии 1,2 км на восток—юго-восток от изб Кулика, по азимутам 0°, 90°, 180° и 270° (магнитное склонение ≈ +4°). Замеры азимутов поваленных стволов с округлением до 5° проводились в полосе шириной до 10 м вдоль радиальных маршрутов и второй половины восточного лесотаксационного разреза и на всех лесотаксационных пробных площадях в 0,25 га. В приводимых ниже расчетах данные по западному лесотаксационному разрезу использованы не были. Для каждой пробной площади или отрезка радиального маршрута длиной около 0,5 км подсчитаны средние азимуты и дисперсии
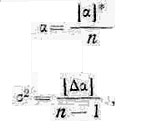
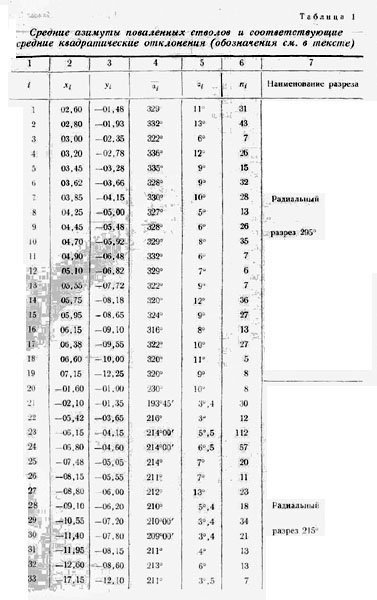
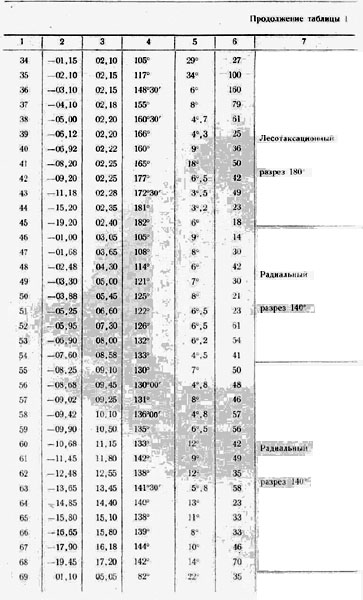
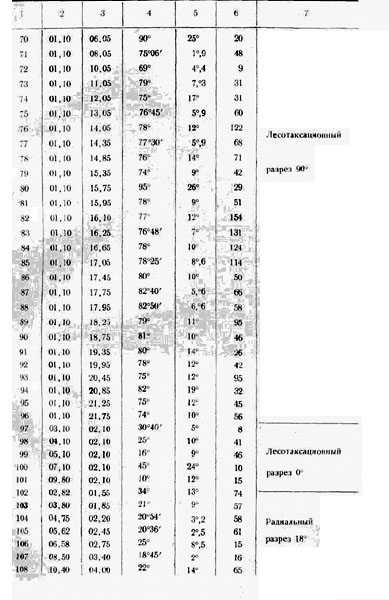
где а1 а2,...,аn — азимуты стволов поваленных деревьев и Δаn = ak- а. При этом учитывалось только около 90% азимутов, группирующихся около наиболее часто встречающегося. В отдельных случаях азимуты группируются в двух направлениях. Это характерно, например, для ряда пробных площадей южного лесотаксационного разреза и в конце радиального маршрута 140° (Здесь и ниже употребляется принятое в способе наименьших квадратов гауссов-ское обозначение суммы [a] = а1 +а2 +....+an 7). В этих случаях подсчитывались два средних азимута по соответствующим группам. В дальнейшем использовался только средний азимут, принадлежащий преобладающей группе деревьев, поваленных взрывной волной. Вторичное направление повален ных стволов, обычно восточное, объясняется преобладающим направле нием ветров. Таким образом, на основании 4620 замеренных азимутов поваленных деревьев были получены 108 средних азимутов аi с соответствующими дисперсиями σ2i (табл. 1).
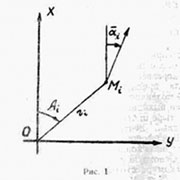
Пусть хОу - прямоугольная си -стема координат (рис, 1), у которой ось x-ов направлена по магнитному меридиану, а начало О -предполагаемый эпицентр взрыва. Качественное рассмотрение картины вывала леса показало, что эпицентр взрыва должен находиться юго-западнее изб Кулика. За начало ко ординат была принята некоторая точка О. В этой системе г. Фарринг-тон имеет, например, координаты Хф = 3,1 км;Уф = 3,1 км. Обозначим точки с координатами хi уi ,для которых на основании пi замеров определены ai и σ2i через Мi .Пусть их полярные координаты будут Аi ri, где за полярную ось взята Если через каждую точку Мi про-х-ов под углом αi ,то их уравнения
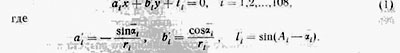
Система (1) представляет собой систему 108 условных уравнений с двумя неизвестными х, у. Для нахождения вероятнейших значений этих неизвестных проведем уравнительные вычисления по способу наименьших квадратов [4]. Условные уравнения (1) составлены на основании неравноточных наблюдений, т. е. средние отклонения t'i., i = 1,2,...,108 неодинаковы (средние отклонения l`i, i= 1,2,,.., 108 приближенно равны средним отклонениям аi, так как Ai- аi малы и можно считать sin(Ai — аi) ≈ Аi—аi ,а средние ошибки Ai- гораздо мень ше средних отклонений аi). Следовательно, уравнения (1) необходимо привести к одинаковому весу. Так как каждое уравнение в (1) имеет вес
![]()
то уравновешенная система имеет вид
![]()
где
Как известно, [3| координаты г. Фаррингтон φ=60°54'58", 98; λ -= 101°56'59", 70.
В нашей системе координат хОу смещение эпицентра относительно г. Фаррингтон можно выразить в виде
Δх = хэ - хф,
Δу = уэ — уф,
где хэ , уэ - координаты эпицентра, а хф, уф - координаты г. Фаррингтон в системе хОу. Так как магнитное склонение ε= + 4°, то по формулам поворота осей координат найдем смещения эпицентра относительно г. Фаррингтон Δх'= —2,3 км, Δу'=—3,2 км, соответственно по долготе и широте. Учитывая, что длина одной минуты меридиана равна 1852 м, а одной минуты параллели — 1852 cos φ м, находим для эпицентра взрыва Тунгусского метеорита координаты φ = 60°53',7; λ = 101°53',5.
Малая величина главного эллипса отклонений единицы веса и рассмотрение картины вывала позволяют сделать вывод о том, что вывал имеет довольно правильный радиальный характер и может быть следствием одного центрального взрыва. Если этот взрыв и сопровождался рядом других взрывов (такой вывод можно сделать, например, по показаниям очевидцев [3, 5]), то они не сыграли какой-либо существенной роли в общей картине разрушений. Вычислительная работа была выполнена участниками экспедиции и рядом товарищей, ранее с экспедицией не связанных. В проведении ее приняли участие Л. И. Лагутская, А. Б. Ошаров, Г. И. Бабецкий, Г. И. Тяпкина, А. Г. Ильин, Г. Ф. Карпунин, Л. К. Ткаченко, Н. В. Васильев, Ю. А. Львов, Г. Ф.Плеханов, В. М. Кувшинников, Г. М. Иконникова, Н. И. Некрытов, В. В.Ма-тушевский, В. И. Мильчевский, А. С. Ероховец, А. И. Ерошкина, Т. М. Тибилова, Н. П. Родионова, Т. М. Слета. Позднее уравнительные вычисления были повторены Л. В. Головяшкиной и А. П. Бояркиной на электронной счетной машине М20.
ЛИТЕРАТУРА
1. Л А. Кулик, 1939. Данные по Тунгусскому метеориту к 1939 году. ДАН СССР, т. XXII, № 8, стр. 520—524.
2. Л А Кулик, 1940. Метеоритная экспедиция на Подкаменную Тунгуску в 1939 году. ДАН СССР, т. XXVIII, № 7.
3. Е. Л. Кринов, 1949. Тунгусский метеорит, М.—Л.
4. А. С. Чеботарев, 1958. Способ наименьших квадратов с основами теории вероятностей, М.
5. А. В. Вознесенский, 1925. Падение метеорита 30 июня 1908 г. в верховьях реки Хатанги, «Мироведение», т. 14, № 1.
