КАРТЫ ВЫВАЛА
В первой части настоящего повествования рассказано, как в экспедиции 1961 года участники радиальных маршрутов установили, что лес, поваленный Тунгусской катастрофой, ограничен контуром, имеющим крыловидную форму, напоминающим очертания ночной бабочки. Уже тогда стало ясно, что это открытие несет в себе ключ к пониманию механизма Тунгусского взрыва. И участники дальнейших экспедиций не жалели сил для детального исследования структуры лесоповала и точного установления его границ:
Чтоб спектроскопов чуткий глаз
И контур сваленного леса
В конце концов открыл для нас
Полог таинственной завесы!
Вывал:излом у корня.
Фото В. Фаста, 60-е гг
Во второй половине 60-х годов на одном из стендов павильона "Космос" Выставки достижений народного хозяйства в Москве посетители видели не совсем обычную схему в виде бабочки, испещренной стрелками. Это была векторная карта вывала леса, произведенного взрывом Тунгусского метеорита. Выполненная лучшими художниками-оформителями Всесоюзной выставки, на стенде она выглядела совсем иначе, чем те истертые планшеты и кальки, которые заполнялись работниками КСЭ под жгучими лучами июльского солнца под звон комариных ансамблей или под моросящим дождем на обрывах Хушмо, у подножья Шахормы, на склонах хребта Сильгами...
Карта вывала леса, конечно, мало что говорила посетителям выставки. Неизмеримо более сильное впечатление производили стоявшие рядом макеты "технометеоров", созданных землянами для вхождения в атмосферы Венеры и Марса, для торможения в кислородной оболочке Земли...
И все-таки у стенда "Тунгусский метеорит" также останавливались посетители выставки. Среди них были и те, кто только что создавал фрагменты этой карты — в тайге, за рабочим столом, у терминала ЭВМ...
Работа по составлению полного каталога и карт вывала леса в районе Тунгусской катастрофы, начатая в экспедиции 1961 года, продолжалась в экспедициях 1963, 1964, 1965, 1968, 1969, 1971, 1977, 1978 и 1979 годов. Изучение вывала леса многие годы было одним из центральных направлений полевых работ КСЭ. В упомянутых экспедициях по программе картирования и описания вывала 1908 года всего участвовало 122 человека. Среди них был и "золотой фонд" специалистов по вывалу — невиданной до того специальности. Это были люди, работавшие по программе "Вывал" в течение нескольких сезонов. Небольшие группы проводили также изучение вывала в контрольных районах — в местах больших ветровалов, созданных ураганами уже в наши дни. Один такой ветровал прошел и по тайге, выросшей на месте вывала 1908 года — вблизи заимки Кулика.
Вывал: дерево, расщепленное ударной волной
Фото В. Фаста, 60-е
Полевые дневники отрядов "вывалистов" обрабатывались в Томске. Бесконечные колонки цифр поступали на вычислительные машины. Огромный труд по проведению всей черновой работы, связанной с расчетами на ЭВМ, взяла на себя Алла Петровна Бояркина, научный сотрудник Института прикладной математики и механики при Томском университете. Составление математических программ, их отладка, проверка, анализ ошибок, нанесение данных на перфокарты — вся эта не романтическая, невидная, но необходимая работа многие годы выполнялись А. П. Бояркиной. Конечно, вместе с добровольными помощниками. Кроме этого, А. П. Бояркина руководила несколькими программами исследований Тунгусской проблемы. Без нее нельзя было также обойтись при практической подготовке экспедиций: решение финансовых головоломок, отбор людей и формирование отрядов, хозяйственные заботы (продовольствие, палатки, тара...). Штаб экспедиции, включая командора, будучи погруженным в хозяйственные, стратегические и математические проблемы, не в силах объять необъятное, иногда отмахивался от неизбежно возникавших проблем, связанных с "человеческим фактором", — ладно, как-нибудь образуется... И эти проблемы как-то сами собой оказывались в поле зрения Аллы Петровны. Именно она иногда ставила вопрос перед руководителем КСЭ о том, что тот или иной работник не подходит КСЭ — не как специалист, а по своим человеческим качествам. Это бывало редко, но когда бывало, Бояркина становилась непримиримой...
Вывал: выворот с корнем
Фото В. Журавлева, 60-е гг
Первая карта вывала, отразившая картину поваленного леса, была построена по данным каталога, включающего сведения по 650 пробным площадям, распределенным по всему району разрушений. В каталоге содержалась информация о 60 000 поваленных деревьях. Для каждой пробной площади было определено среднее направление поваленных деревьев, которое и наносилось на векторную карту вывала. Эта карта была опубликована в 1964 году в "Метеоритике". Статья, содержащая анализ вывала Тунгусского взрыва, была написана совместно представителями Комитета по метеоритам и КСЭ. Фамилии авторов решено было перечислить в алфавитном порядке: Бояркина, Демин, Зоткин, Фаст.
ПЕРВАЯ ДИССЕРТАЦИЯ
По мнению В. Фаста, проделанная работа была не итогом исследования вывала, а лишь началом длинного пути. Каталог содержал огромное количество разнообразной информации о катастрофе, только небольшая ее часть была отражена в векторной карте повала деревьев. Однако для изучения этой информации, для ее извлечения и интерпретации требовалась огромная работа. Фаст обратился к своему научному руководителю с просьбой сменить ему тему диссертации — он предлагал, чтобы кафедра математического анализа ТГУ вместо исследования свойств многолистных функций включила в свои планы статистические исследования вывала Тунгусского метеорита. Столь несерьезное предложение никогда, разумеется, не нашло бы понимания, если бы не письмо академика М. А. Лаврентьева, в котором подчеркивалась важность исследования Тунгусского взрыва.
Диссертация аспиранта В. Г. Фаста "Статистическая структура полей разрушений, вызванных ударной волной Тунгусского метеорита" была защищена в 1966 году. Защита прошла успешно, ученый совет единогласно голосовал за присуждение молодому ученому степени кандидата физико-математических наук. Это была первая диссертация, защищенная по проблеме Тунгусского метеорита. Она до сих пор является непревзойденным исследованием механических следов Тунгусского взрыва, "энциклопедией вывала". Ее содержание было частично опубликовано в статьях Фаста, помещенных в "Метеоритике", сборнике "Проблема Тунгусского метеорита" 1967 года и других изданиях. Следует подчеркнуть, что Фаст очень осторожно подходил к истолкованию результатов своих исследований. Свою задачу он видел не в объяснении Тунгусского явления, а в научно грамотном описании его следов. Он любил цитировать известное заявление Ньютона: "Гипотез я не изобретаю". Именно поэтому результаты его математического исследования полей разрушений Тунгусского взрыва являются фундаментом для физиков, изобретающих подчас противоположные, несовместимые гипотезы о механизме и природе этого явления.
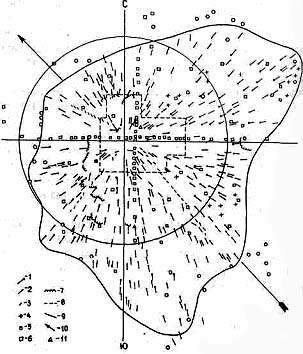Рис. 8. Векторная карта вывала леса: 1 — замеры 100—150 деревьев; 2 — замеры нескольких деревьев; 3 — замеры вдоль маршрутов; 4 — вывал не заметен; 5 — вывала нет, старый лес; 6—лесотаксационные пробные площади; 7 — распространение пожаров; 8 — граница аэрофотосъемки 1938 года; 9— граница вывала; 10—траектория по Кринову; 11 — гора Фаррингтон. ("Метеоритика". 1964. Вып. 24.)
Одна из первых физико-математических задач, блестяще решенных Фастом, — это установление связи между степенью статистического разброса направлений повала деревьев и физической силой, действовавшей на них. Он нашел строгое математическое доказательство того, что лес, поваленный ударной волной, может быть использован вместо измерительного прибора для определения скоростного напора воздуха, идущего за ударной волной.
Под действием аэродинамического давления дерево падает не строго в том направлении, куда направлена сила. Сила действует, в первую очередь, на крону, а она у каждого дерева имеет свою собственную форму. Сила действует и на ствол, и в зависимости от его диаметра давление на деревья оказывается разным. Наконец, длина и расположение корней, свойства почвы в каждом данном месте, особенности рельефа, влияние соседних деревьев и так далее — все эти многочисленные причины приводят к тому, что направление повала оказывается случайным вектором.
Точнее, направление упавшего дерева определяется двумя величинами: регулярным давлением фронта ударной волны и некоторым случайным вектором, из-за которого дерево падает не строго в направлении распространения волны. Степень разброса направлений деревьев вокруг среднего значения характеризуется в теории вероятностей средней квадратичной ошибкой, которую специалисты для краткости называют "стандартом". В одной из предыдущих глав мы уже рассказывали, что была обнаружена зависимость "стандарта" от расстояния до центра вывала. В 1960 году эта закономерность была прослежена по шести радиусам.
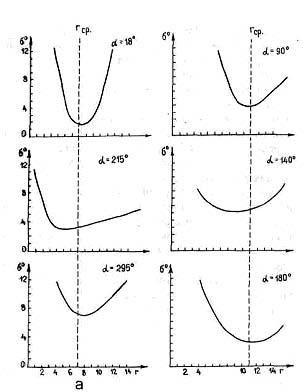Рис. 9. Эффект Демина: зависимость "стандарта" (среднего квадратичного отклонения) вывала от расстояния до эпицентра: а — азимуты, по которым лес валила взрывная волна; б —азимуты, по которым вывал произведен с участием баллистической волны; а —"стандарт" в градусах; r —расстояние в километрах
В результате работ по площадной съемке вывала, проводившихся под руководством Фаста, стало возможным построить поле "стандартов" для всей территории вывала. Закономерность, подмеченная Деминым, выполнялась на всей этой территории. В самом факте зависимости разброса направлений деревьев от расстояния до центра вывала не было ничего непонятного или неожиданного. Конечно, если считать, что источник взрыва был на высоте нескольких километров. Направление вектора силы под источником взрыва было вертикальным — поэтому ударная волна, ободрав ветки деревьев, оставила на корню сами деревья. Там, где направление на источник составляло некоторый угол с вертикалью, кроме вертикальной составляющей силы, появлялась горизонтальная, которая и валила деревья. Вблизи зоны "телеграфного леса" горизонтальная составляющая была очень мала, дальше она увеличивалась. Чем больше была горизонтальная компонента силы, тем правильнее, упорядоченное ложились стволы, тем меньше была величина статистического "стандарта". Расстояние до минимального разброса (стандарта) в разных местах вывала оказывалось различным—от 5 до 12 километров. Дальше от центра взрыва горизонтальная составляющая снова уменьшалась — ударная волна ослабевала с увеличением расстояния.
Соединив на карте распределения стандартов места с одинаковым значением разброса направлений упавших стволов, Фаст получил карту изостандартов. Она оказалась сложной — изостандартные линии повторяли "крылья бабочки" и имели собственную симметричную структуру. Эта структура имела признаки и центральной и осевой симметрии и подтверждала догадку академика Садовского о том, что источник взрыва имел сложную форму.
Вывал: выворот с корнем
Фото В. Журавлева, 70-е гг
Однако Фаста интересовали не эти качественные заключения, а возможность получения количественной информации об ударной волне Тунгусского взрыва. Для этого требовалось дать математически обоснованный ответ на вопрос: какой будет ошибка, если мы будем судить о свойствах ударной волны Тунгусского взрыва (или Тунгусского болида) по степени направленности вывала, используя эту характеристику вместо измерителя давления? В диссертации Фаста эта задача была решена на конкретном материале, полученном группами "вывалистов". Для этого пришлось доказать две теоремы о характере распределения азимутов поваленных деревьев. В результате был сделан важнейший для физики Тунгусского явления вывод:
"Аэродинамическое давление обратно пропорционально стандартному отклонению направлений повала от среднего ".
Это равенство было приближенным. Анализ маршрутных дневников и расчет на ЭВМ показали: при стандартных отклонениях, меньших 16°, суммарная ошибка при пользовании формулой Фаста не превышает 2,5%. То есть практически на всей территории вывала изостандартные линии с точностью хорошего физического прибора дают представление о величине силы, валившей деревья! Линии равных сил называют изодинамами. Итак, карта изостандартов поваленного леса оказалась картой изодинам. Уничтоженная Тунгусской катастрофой тайга хранила, как оказалось, точную количественную информацию о "госте из Космоса".
В работах Фаста были построены и проанализированы с точки зрения математики и другие поля ударной волны Тунгусского метеорита: линии тока изохроны ударной волны, изоклины... Была построена карта распределения стоящих мертвых деревьев которая внесла серьезные поправки в хорошо известную схему: "в центре — стоячий лес, а дальше — радиальный вывал". Эта схема была верной, но упрощенной. В самом деле, в прямоугольнике 14 на 5 километров плотность "телеграфного леса" была примерно 140 деревьев на гектар. Следующая изолиния (расстояние до нее—от центра телеграфного леса в разных направлениях различно) соединяет места с плотностью 60 столбов на гектар. Странно, но факт — эта изолиния не замыкается, а тянется на запад далее 20 километров... Неожиданная картина вырисовывается и на востоке: оказывается, стоячие деревья 1908 года попадаются и в зоне "сплошного вывала", правда, их средняя плотность здесь только 20 столбов на гектар. Изолинии вырисовывают сложный симметричный узор. Некоторые юмористы увидели в их очертаниях изображение пальца, указывающего направление полета тела... К сожалению, физики так и не решились проанализировать карту стоячего леса. По-видимому, потому, что из нее следовали выводы, которые не вписывались в простую модель явления. Дело ограничилось юмором.
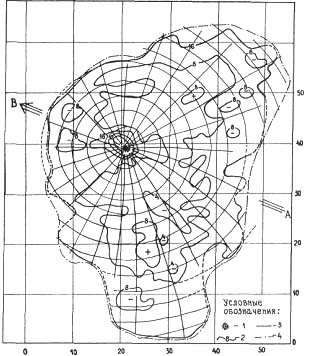Рис. 10. Структура "бабочки вывала", рассчитанная В. Г. Фастом: изостандартные линии, оказавшиеся изодинамами — линиями равных аэродинамических напоров. Цифры обозначают величину среднего квадратичного отклонения поваленных деревьев от среднего азимута повала в градусах. АВ — первая траектория Фаста (линия осевой симметрии) 1 — эпицентр, 2 — изостандарты, 3 — линии фронта ударной волны и направления движения этого фронта, 4 — граница вывала леса. Знак плюс внутри замкнутых изолиний показывает, что разброс направлений стволов на этой площади больше, чем на изолинии, знак минус — меньше
Фаст рассчитал точку, в которой пересеклись бы продолжения средних направлений поваленных деревьев. Положение этой точки на местности удалось определить с точностью 200 метров. Она пришлась на ничем не примечательное место — небольшой мыс на северном берегу Южного болота у подножья горы Стойкович. Когда-то это место, как и гора, было сплошь занято "телеграфным лесом". Теперь столбы лежат в беспорядке на земле, а к небу тянутся молодые сосны и лиственницы. Рассчитанную математическую точку центра радиального вывала стали называть эпицентром. Фаст считал это название не вполне корректным и предпочитал более осторожное название — "особая точка вывала". Участникам экспедиции не нравилось столь длинное название, и в бытовом обиходе центр вывала стали называть просто "эпифастом".
Физический смысл особой точки вывала баллистики определили очень просто — это точка, где ударная волна, пришедшая сверху, впервые коснулась поверхности земли. То, что ее координаты удалось рассчитать с точностью до 200 метров, указывало на то, что источник взрыва был небольшим — во всяком случае, много меньше, чем поперечник зоны стоячего леса. На аэрофотоснимках Кулика видно, что направленный вывал существовал и в пределах этой зоны. Наземные наблюдения, проводившиеся в послевоенных экспедициях Зоткиным, Фастом, Деминым, Голенецким, еще раз подтвердили этот вывод. Уже на первом километре от эпицентра действовала заметная горизонтальная составляющая воздушного напора.
"Телеграфный лес" в центре катастрофы. Деревья с уничтоженной кроной долго боролись за жизнь: тонкие веточки на стволах выросли после 1908 года.
Фото В. Журавлева I960 г
ЦЕНТР И ЕЛОЧКА
Первый детальный физический анализ бабочки вывала был проведен А. В. Золотовым. Несмотря на некоторые трения между томичами и башкирцами, результаты первичной обработки полевых дневников "вывалистов" передавались Золотову задолго до их публикаций. Золотов анализировал лишь векторную карту вывала — другие карты в то время еще не были готовы. Золотов был первым, кто обнаружил на карте радиального вывала эффект второго порядка — осесимметричные отклонения от строгой радиальности. Проведя статистический анализ этих отклонений, он показал, что они выходят за пределы случайного разброса. Золотов сделал вывод, что осесимметричные отклонения от радиальности, которые имеются лишь в юго-восточной части вывала, представляют собой след действия баллистической ударной волны. Мера отклонения вывала леса от строгой радиальности является мерой мощности баллистической волны.
Для расчета действия баллистической волны Золотов использовал формулы цилиндрического взрыва, полученные В. П. Коробейниковым. Расчет позволил обнаружить зону максимального действия баллистической волны, которая проходила на расстоянии от 7 до 14 километров от эпицентра. Даже в этой зоне баллистическая волна не была достаточно мощной, чтобы валить деревья. Она лишь изменила направление фронта взрывной волны. Первое объяснение двукрылой формы границы вывала было дано Золотовым на основе почти очевидной модели: сферический взрыв произошел внутри конуса баллистической волны. Тело, летящее в воздухе со скоростью, большей скорости звука, порождает вокруг себя баллистическую волну в виде конуса. Угол раствора этого конуса вполне определенный: он зависит только от отношения скорости баллистической волны к скорости тела.
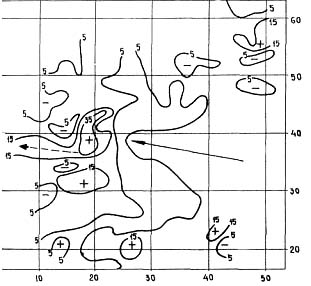Рис. 11. Изолинии "телеграфного леса". Цифры показывают число стоящих мертвых деревьев на пробной площади (0,25 га). Незамкнутая изолиния 15 на западе—намек на "взлет" (пунктирная стрелка). Резко изогнутая изолиния 5 на востоке — "палец", указывающий проекцию траектории (сплошная стрелка). Знак плюс указывает, что плотность стояков на площади, ограниченной изолинией, больше, чем на этой границе, знак минус — меньше
Используя это соотношение, Золотов нашел скорость Тунгусского космического тела. При этом он использовал тот реальный след, который баллистическая волна оставила на поваленной тайге в виде нарушений радиальности вывала в тех местах, где сферическая волна пересекла конусообразную. Построив "кинофильм", реставрировавший движение волн через каждые 5 секунд после взрыва и использовав метод последовательных приближений, Золотов получил, что средняя скорость Тунгусского объекта на конечном участке траектории длиной около 18 километров была всего 1—2 километра в секунду, т. е. не превышала скорость реактивного самолета.
Из расчетов Золотова следовало; что энергия баллистической волны не превышала 9·1020 эрг, полная энергия взрыва составляла от 2·1023 эрг до 6·1023 эрг, поперечные размеры тела были порядка 50 метров, максимальная протяженность взрыва вдоль траектории не более 600 метров. Кинетической энергии тела при той скорости, которая следовала из расчетов, было недостаточно для тех разрушений, которые оставил на земле необычный метеорит. Следовательно, взрыв произошел за счет выделения внутренней энергии тела. Золотов считал, что это была ядерная энергия, в таком случае масса прореагировавшей ядерной взрывчатки составляла 400 кг.
Золотов был уверен, что ось симметрии бабочки вывала — это проекция траектории Тунгусского тела на поверхность Земли. Соглашаясь с этим выводом, В. Г. Фаст формулировал его более осторожно: "Представляется наиболее вероятным связать (а может быть, и отождествить) выявленную ось симметрии с проекцией траектории метеорного тела на земную поверхность ". В 1967 году эта осторожность в выражениях воспринималась просто как дань академическому стилю изложения. В 80-х годах, когда исследователи, наконец, попытались связать траекторию, найденную по бабочке вывала, с траекторией, указанной очевидцами, пришлось признать, что эта осторожность была далеко нелишней...
Золотов доказывал, что эпицентр, определенный Фастом, является лишь формальной математической точкой. Истинный эпицентр взрывной волны, по его расчетам, следовало сместить на 1,5 км от "эпифаста" к северо-западу, этого требовала физическая модель явления, которая основывалась на взаимодействии баллистической и взрывной волн.
Золотов раскритиковал модель облака космической пыли, показав, что при взрыве такого облака или роя, размер области взрыва был бы значительно больше и что "почти точечного" эпицентра не могло получиться. Золотев был не согласен и с расчетом профессора К. П. Станюковича, построившего схему теплового взрыва ледяного тела. По Золотову, эта модель могла бы быть хоть как-то согласована с реальной картиной вывала, только если приписать Тунгусскому телу плотность ртути —14 г/см3 или выше. При плотностях же от 1 до 8 г/см3 (лед, силикат, железо) карта вывала указывает на то, что размер источника был порядка 0,5 км, а скорость ниже 5 км/с. Так, если бы над тайгой на высоте 10 км со скоростью 30 км/с летело ледяное тело массой 100 000 тонн, поперечником 50 м, то оно произвело бы полосовой вывал леса в виде "елочки". Ширина полосы поваленного леса была бы около 100 километров. На самом деле вывал был радиальным, а "елочка" проявлялась лишь как слабый эффект второго порядка. Золотев предполагал, что можно обнаружить "эффекты третьего порядка", если более детально и с большей точностью провести измерения направлений поваленных деревьев в определенных районах вывала. Тогда можно восстановить форму взорвавшегося тела. В. Фаст считал постановку такой задачи просто неграмотной, так как точность проведенных измерений ограничивалась случайным разбросом азимутов.
А БЫЛ ЛИ ВЗРЫВ?
Однако, казалось бы, неуязвимая научная позиция Фаста была поставлена под сомнение студентом Томского университета Джоном Анфиногеновым. Джон Федорович Анфиногенов унаследовал от своих родителей не только английское имя (его отец, строитель ДнепроГЭСа, подружился на этой стройке с американским инженером и назвал сына Джоном ради советско-американской дружбы). Он унаследовал еще и кипучую, бурную энергию, жадность к работе и знаменитый принцип "подвергай все сомнению". Он подвергал сомнению даже принципы квантовой механики, в связи с чем не мог найти общего языка с преподавателями университета. Его подход к любому вопросу удивлял своей неожиданностью и странностью. Он обладал способностью видеть то, чего другие не видели. Сталкиваясь с постоянным непониманием и недоверием к своим открытиям, он потерял всякую надежду переубедить критиков и, изложив свою точку зрения, никогда не тратил время на то, чтобы довести начатое, например, до публикации. Поняв что-то, как он считал, до конца, Джон Федорович терял интерес к вопросу и начинал думать над новой загадкой.
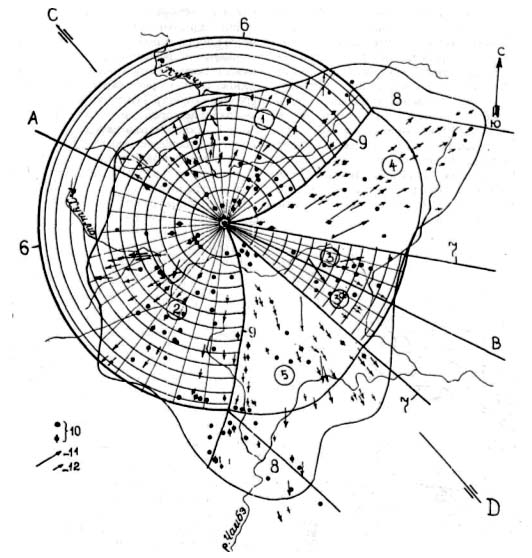
Рис. 12. Анализ картины вывала в районе Тунгусского взрыва по А. В. Золотову. В А —траектория по Золотову, DC-no Кринову. 1—3 — области строго радиального вывала сферической ударной волной; 4—5 — области суммарного действия взрыв ной и баллистической волн; 6— фронт взрывной волны; 7— фронт баллистической волны в момент взрыва; 8 — фронт баллистической волны в момент встречи с взрывной волной в 25 км от эпицентра; 9 — граница между областями со строго радиальным и осесимметричным вывалом; 10 — поваленные деревья, направление которых проходит через эпицентр взрыва; 11 — направления поваленных деревьев, которые отклоняются от эпицентра хаотически; 12 — на правление поваленных деревьев, систематически отклоняющихся от направления на эпицентр, т. е. соответствующих осевой симметрии
Вывал и новый лес у вершины горы Стойкович
Фото 1973 г
Взглянув на карту вывала Фаста, Анфиногенов поставил под сомнение вопрос о центральном взрыве, хотя наличие эпицентра и строгой радиальности повала отвергать было невозможно. "А был ли взрыв?" — тем не менее спрашивал он. В этом он как раз не был оригинальным. Московские астрономы и физики (Зоткин, Бронштэн, Станюкович, Цикулин) в те же годы, да и позднее, пытались объяснить бабочку вывала как результат действия мощной баллистической волны. Сложилось два противоположных подхода к истолкованию картины вывала. С кометной гипотезой лучше совмещалось такое истолкование: вывал был результатом мощной ударной волны, вызванной торможением тела в атмосфере, т. е. баллистической волной. Станюкович, Цикулин, Анфиногенов считали, что привлекать еще какой-то дополнительный взрыв вообще излишне. Бронштэн и Зоткин допускали, что дробление и испарение кометного ядра в конечной точке траектории могло породить взрывную волну, которая сложилась с баллистической, но была слабее ее или того же порядка мощности.
Золотов, как мы видели выше, считал, что скорость тела была не настолько большой, чтобы вызвать баллистическую волну, способную валить деревья. Взрыв был сферическим, его источником была внутренняя энергия тела, но поскольку он был окружен конусом баллистической волны, то энергия сферического взрыва была направлена больше в стороны, а не в направлении полета тела. Золотов рассмотрел и вторую причину, по которой могла возникнуть бабочка, — форма оболочки взорвавшегося тела. Он считал, что та направленность "крыльев" взрыва, которая была при Тунгусском взрыве, могла иметь место, только если размеры оболочки составляли 2—3 километра. Это противоречило оценке поперечных размеров тела, сделанных по картине вывала,— они были не более 50— 70 метров. Следовательно, "оболочка", считал Золотов, могла быть только воздушной — зоной сжатия конуса баллистической волны. Ее размеры достаточны, чтобы создать эффект направленности взрыва на всей площади разрушений.
Истолкование следов ударной волны Тунгусского тела с точки зрения кометной гипотезы требует высоких скоростей тела и крутой траектории (скорость от 20 до 40 км/с, угол наклона к горизонту пути тела 30—60°). Приведем эту точку зрения в изложении И. Т. Зоткина (цитируем "Астрономический календарь" за 1965 год).
"Баллистическая волна, образуемая в воздухе телом, движущимся со сверхзвуковой скоростью, сопровождается грохотом, ударами и гулом. Баллистическая волна, как и взрывная, является резким скачком уплотнения в воздухе, но вызванным не расширением продуктов взрыва, а сверхзвуковым движением тела. В пространстве баллистическая волна имеет вид конуса. При астрономических скоростях эта волна имеет форму цилиндра, и ее можно моделировать взрывом цилиндрического заряда взрывчатого вещества.
Ядро кометы, как и всякое метеорное тело, на высотах ниже 100 км образовало болид, путь которого в атмосфере имел не менее 500 км. Энергия тела расходовалась на плавление и пульверизацию вещества, испарение, свечение и ионизацию. В нижнем участке траектории значительная энергия расходовалась на образование баллистической волны, которую очевидцы ощущали в виде ударов. Плавление и испарение было настолько бурным и интенсивным, что до высоты 10—20 км израсходовалось не менее половины массы.
На этих высотах аэродинамический напор встречного потока воздуха достигает огромной величины — тысяч атмосфер. Даже прочные каменные и железные метеориты при этом обычно дробятся. Рыхлое ледяное тело, каким представляется ядро кометы, в таких условиях будет буквально раздавлено. Произойдет прогрессивное, почти мгновенное дробление быстро движущегося тела. Резко увеличившаяся площадь поперечного сечения вызовет резкое усиление баллистической волны. Одновременно произойдет резкое увеличение светоотдачи болида, которое наблюдатель воспримет как яркую вспышку. Весь этот процесс, происшедший за доли секунды, по существу представляет собой взрыв, который в отличие от теплового и химического можно назвать механическим взрывом. Возможно, он был усилен распадом неустойчивых химических веществ типа радикалов, которые присутствуют в кометах ".
МОДЕЛЬ БАБОЧКИ
И. Т. Зоткин и М. А. Цикулин пытались экспериментально подкрепить защищаемую ими теоретическую схему. Начиная с 1966 года, они провели серию модельных лабораторных экспериментов. В их опытах использовался детонирующий шнур, выделявший при взрыве 6•109 эрг/см. В конце шнура помещался сферический заряд из гексогена, взрыв которого должен был моделировать завершающую вспышку и возникновение сферической волны. Наклон шнура соответствовал разным вариантам наклона траектории к горизонту. Деревья заменялись гибкими неупругими проволочками высотой 3 см, у них была цилиндрическая "крона" из пластика.
Когда экспериментаторы подрывали заряд, проволочки гнулись, указывая направление фронта ударной волны на площадке под детонирующим зарядом. Опыты закончились успехом — очертания зоны разрушений походили на Тунгусскую бабочку! Наиболее близкое сходство модельного поля с Тунгусским вывалом было достигнуто при наклоне шнура к горизонту около 30° и усилении мощности взрыва на конце шнура в четыре раза. Эти эксперименты произвели впечатление на исследователей Тунгусской проблемы и многими воспринимались как успех кометной гипотезы. То, что модель не воспроизводила многие важные особенности Тунгусского вывала, не тревожило ни авторов эксперимента, ни других сторонников кометной модели. Любое моделирование не способно воспроизвести все особенности изучаемого явления. Оно повторяет лишь главное в нем. А вот что главное — на этот счет могут быть очень разные точки зрения.
При моделировании Тунгусской бабочки не выполнялись законы подобия хотя бы потому, что наиболее близким аналогом взрыва Тунгусского болида мог быть только небольшой ядерный взрыв. Размер заряда во взрывной камере Цикулина был несоизмеримо больше относительного размера Тунгусского тела. Поэтому точечного эпицентра в опыте не могло получиться. Осесимметричные эффекты также были намного сильнее. Если же сравнивать модельный вывал не с векторной картой Тунгусского вывала, а с картой изодинам и с картой стоячего леса, рассчитанных Фастом, то сходство модели и натуры станет еще меньше. Опыты Зоткина и Цикулина следовало рассматривать лишь как первый шаг в экспериментальном изучении вывала. Однако после первого успеха — воспроизведения в первом приближении контура границ вывала — эксперименты были прекращены. Задача восстановления формы заряда по картине вывала даже не ставилась.
В 1969 году в издательстве "Наука" вышла книга М. А. Цикулина "Ударные волны при движении в атмосфере крупных метеоритных тел". В ней излагался метод анализа баллистической волны большого метеорита на основе теории цилиндрического взрыва. Разработанный Цикулиным физико-математический аппарат применялся для анализа ударных волн Тунгусского метеорита по данным каталогов вывала. Цикулин использовал и результаты Золотова. Так, он принял предложенную Золотовым модель объяснения двукрылой структуры вывала на основе рассмотрения взрыва в конусе баллистической волны как наиболее простое и естественное объяснение.
Но расчеты, проведенные на основе собственной теории цилиндрического взрыва, привели Цикулина к иным выводам по сравнению с Золотовым. При тех же исходных данных Цикулин получил, что амплитуда взрывной волны была больше амплитуды баллистической волны всего на 35%. Это совпадало с результатом модельного эксперимента и резко отличалось от цифр, полученных Золотовым. По Золотову, баллистическая волна была в десять раз слабее взрывной.
Расчеты Цикулина подводили фундамент аэродинамики под здание кометной гипотезы. Расчеты Золотова доказывали, что возможен совершенно иной подход к истолкованию полевых данных по вывалу. Две первые научные монографии по Тунгусской проблеме с противоположной трактовкой фактов вышли в свет одновременно — в 1969 году. Однако каких-либо диспутов по поводу расхождений не было. Книга Цикулина расценивалась в тех научных кругах, которые так или иначе соприкасались с проблемой Тунгусского метеорита, как профессиональный труд специалиста-газодинамика, книга Золотова — как сочинение увлеченного дилетанта, опубликованное по недосмотру ученого совета. Никто не обратил внимания на очень существенную разницу в подходах обоих авторов к проблеме, которая заключалась в разном отношении к фактическому материалу. Золотов провел детальнейший анализ векторной карты вывала и пытался воссоздать существенные черты явления по имевшемуся массиву фактов. Кроме того, он анализировал не только вывал, но и сейсмические, барические, магнитосферные возмущения, связанные со взрывом, стараясь создать цельную картину явления.
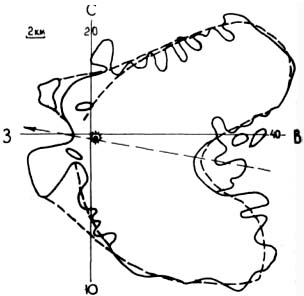Рис. 13. "Бабочка Анфиногенова" — контур послекатастрофного леса, выявленный по аэрофотоснимкам. Пунктиром проведены варианты сглаженного контура. Система координат —по В. Г. Фасту. Пунктирная стрелка — проекция траектории
В книге Цикулина Тунгусская проблема рассматривалась скорее как пример, иллюстрирующий теорию цилиндрической ударной волны. Огромный фактический материал о разрушениях в тайге был использован в минимальной степени. Автора не интересовали сложности и противоречия картины взрыва, он отбирал для анализа лишь очевидное. Золотову для окончательных выводов часто не хватало фактов, Цикулину большая часть фактов, добытых экспедициями, просто не пригодилась.
ВЕРЕТЕНО
Одновременно с Цикулиным и Золотовым вел анализ карты вывала Д. Ф. Анфиногенов. Отвергая фантастику и романтические домыслы, он был уверен, что проблема должна решаться на базе реализма и конкретных фактов. Его методология может быть охарактеризована ломоносовским афоризмом: "Природа весьма проста, что этому не отвечает, должно быть отвергнуто".
Анфиногенов рассматривал дробление гигантского метеорита. Выводы о точечном взрыве, не оставившем материальных следов, он считал заблуждением, основанным на ошибочной трактовке явления. Не будучи специалистом-газодинамиком, Анфиногенов изучил классические работы и новейшие статьи по разрушению тел, входящих в атмосферу с космическими скоростями, и, конечно же, нашел собственные оригинальные решения некоторых вопросов метеоритного сопромата*.
Он тщательно изучил аэрофотоснимки района Тунгусского падения, сделанные с лесохозяйственными целями. Эти снимки держали в руках и до него разные специалисты, но вывал на них был не виден — новая тайга закрыла его следы сплошным пологом. Да и масштаб аэрофотоснимков не был рассчитан на изучение лесоповала.
Но Анфиногенову пришла в голову простая и гениальная идея. Перед поступлением в университет он успел поработать дешифровщиком аэрофотосъемки и знал, что даже на черно-белых снимках лес разного возраста выглядит по-разному. Конечно, эту разницу может уверенно уловить лишь специалист. И Джон Федорович, забыв про надвигавшуюся экзаменационную сессию, начал кропотливую обработку снимков. Ее итогом явился контур района, заросшего лесом послекатастрофного поколения.
Этот контур имел форму бабочки. В чем-то бабочка Анфиногенова повторяла бабочку Фаста, в чемто имела собственные особенности. Размах ее крыльев был меньше, чем тот, который устанавливался по крайней границе вывала. Анфиногенов сумел получить независимую информацию о Тунгусском взрыве. Тайга, как гигантская фотопластинка, запомнила один из моментов катастрофы, записала контур воздушной волны, сметавшей все живое.
Рис. 14. "Веретено Анфиногенова" — схема распределения энергии по высоте при разрушении Тунгусского метеорита. Е — энергия, h — высота, r — расстояние от эпицентра Фаста. Штриховкой выделены зоны с разной интенсивностью энерговыделения при приближении болида к поверхности Земли: I — потеряно 20% энергии и массы, II, III — около 80% (III — максимум энерговыделения), IV — остаточное энерговыделение вплоть до высоты 2 км
Сравнивая контур живого леса, выросшего на месте погибшего, с контуром изодинам, Анфиногенов пришел к подозрению, что статистический метод в процессе усреднения данных приводит к потере части сохранившейся информации. Аналогичную мысль, как мы видели выше, высказывал Золотов, но Анфиногенов имел в виду не слабые "эффекты третьего порядка", а гораздо более существенные следы. Споры с "корифеями вывала" не прояснили сути дела, и тогда Анфиногенов начал осуществлять в тайге собственную программу изучения вывала.
Особенно странной представлялась ему картина вывала на северо-западе от эпицентра, где вопреки очевидным аксиомам физики взрыва кинетическая энергия продуктов взрыва не складывалась с кинетической энергией осколков метеорита, а скорее "вычиталась". По направлению движения тела радиус зоны разрушений был минимальным. Это было известно еще Флоренскому, но в свете результатов моделирования это можно было как-то объяснить.
Анфиногенов, обследуя северо-западный сектор вывала, пришел к заключению, что замкнуть изодинамы ударной волны в этом районе вообще нельзя — лес был повален только на вершинах. Однако Фаст проводил на карте изодинам в этом районе сплошные линии. Диспут о законности различных приемов усреднения измеренных характеристик лесоповала был острым и длительным. Он закончился выработкой согласованных мнений и признанием результатов, полученных Анфиногеновым.
Анфиногенов, пренебрегая фактом существования точечного эпицентра, рассчитанного Фастом по средним векторам азимутов поваленных стволов, считал, что источником ударной волны была линия. Ее положение в пространстве он рассчитал по собственной методике, опираясь на реальную картину ориентации поваленных деревьев. К 1966 году была построена следующая схема: — если считать источник взрыва линейным, то угол наклона этой линии к горизонту составлял 40—50°;
— максимальное выделение энергии произошло на высоте 5—7 км;
— выделение энергии происходило еще до высоты 2—4 км;
— суммарная энергия ударной волны—5· 1022 эрг;
— ударная волна имела веретенообразную форму, а не "почти цилиндрическую", как считали все исследователи до этого.
Камень Джона Фото В. Петухова, 1973 г
Последний вывод был неожиданным и с точки зрения аэродинамики метеоритов и с точки зрения модели Золотова. Следует подчеркнуть, что к этому заключению Анфиногенов пришел в процессе решения задачи: как согласовать реальную картину вывала в северо-западном секторе лесоповала с линейной моделью источника взрыва.
"Веретено" диктовалось фактами. Каков же физический смысл столь необычной формы ударной волны? Анфиногенов сделал последнюю в истории Тунгусской проблемы попытку "примирить" Тунгусский взрыв с падением обычного метеорита. Он построил следующую модель: дробление гигантского астероида (каменного или железного) началось на высоте 10—15 км, ниже 10 км ударные волны отдельных обломков слились в единую баллистическую волну, на высотах ниже 4 км кинетическая энергия осколков была уже потеряна, вследствие чего ударная волна резко ослабла.
Опять осколки?
Из этой модели следовало: в 3—5 километрах от эпицентра Фаста произошло выпадение гигантского метеоритного дождя. Следовательно, Кулик допустил только одну ошибку: он искал осколки метеорита в центре лесоповала, так как не знал, как выглядит контур вывала. Кулик был в этом районе, но не заметил здесь ничего примечательного. Самую высокую вершину, находившуюся вблизи места, куда должен был врезаться "метеорит Анфиногенова'', он назвал именем американского геохимика Кларка. В одном километре от нее на берегу болота находится другая сопка, хорошо заметная издали благодаря лысой вершине. Кто-то из участников послевоенных экспедиций назвал ее "гора Острая". Название прижилось, так как эта сопка была удобным ориентиром. Было ли у нее до войны другое название, установить трудно, так как у Кулика не было точной карты**. Именно от западного склона Острой начинается сектор леса площадью в 3 квадратных километра, который Джон Анфиногенов обозначил как место выпадения вещества Тунгусского метеорита. От эпицентра Фаста он находился на расстоянии 5 километров. Для удобства этот район окрестили "эпиджоном".
"Группа свободного поиска", руководимая Анфиногеновым, провела огромную работу в "эпиджоне" и его окрестностях. Тщательно изучались любые камни на вершинах и склонах гор, которые казались хоть чем-то отличающимися от остальных. Раскапывались ямы и подозрительные углубления с валиками, которые были обнаружены вблизи Острой. В конце концов они оказались сгоревшими муравейниками. Анфиногенов собирал коллекцию камней и галек, намываемых ручьями и реками на территории вывала. В ней были кусочки кварца, исландского шпата, туфов, песчаников и, конечно, сибирских траппов — характерных горных пород Среднесибирского плоскогорья. Но никаких следов гигантского метеоритного роя обнаружить не удалось. "Тунгусский метеорит" смеялся в очередной раз над искателем, пытавшимся прилагать к нему обычные мерки...
Но Анфиногенов настойчиво искал подтверждения своей теории. Уже в начале 70-х годов он раскопал на вершине горы Стойкович нетипичный для этих мест многопудовый камень. Джон считал, что он нашел легендарный "камень Янковского". О нем достаточно рассказано в книгах и очерках об экспедициях Кулика. Янковский нашел его в 1930 году и предположил, что это — осколок каменного метеорита. Кулик, искавший железный метеорит, пренебрег находкой своего молодого помощника. После войны Янковский уже не мог вспомнить точное место, где он сфотографировал камень. На поиски знаменитого камня в 60-х годах в КСЭ приезжали тайшетские школьники. Однако прочесывание тайги во главе с "дедушкой Янковским" оказалось безуспешным.
Анфиногенов обратил внимание на не замеченную ими странную "кочку", покрытую мхом. На ней успела поселиться молодая березка. Десятки людей проходили в этом месте мимо "кочки", но только Анфиногенов догадался снять с нее моховой покров. Под ним был камень, не похожий на окружающие его траппы. Раскопки необычной глыбы, предпринятые энтузиастами, однако, не привели к сенсации — геологи легко опознали в камне кварцевый песчаник, типичную земную породу, сформировавшуюся в зоне морского прибоя. Как он попал на вершину потухшего вулкана—гору Стойкович? Это была загадка, но из области исторической геологии, а не метеоритики.
* "Сопромат"— жаргонное, "студенческое" название специального раздела механики — "Сопротивление материалов".
** По-видимому, Кулик присвоил этой вершине имя московского петрографа профессора П. Н. Чирвинского, автора монографии "Палласиты". Однако на географических картах 50-х годов вершина не имеет названия.